 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Код с естественными весами 8-4-2-1
Таблица
Это простейший двоично-десятичный код, в котором каждая десятичная цифра представлена своим двоичным эквивалентом. Выполнение операции алгебраического сложения требует перевода цифр из прямого кода (ПК) в обратный код (ОК) или дополнительный код (ДК). В двоично-десятичной арифметике принято использовать обратный код. Главный недостаток кода с естественными весами 8-4-2-1 в отсутствии свойства самодополняемости. Простое инвертирование тетрад прямого кода образует псевдообратный код, который дополняет исходную тетраду до 15=1111, а для формирования обратного кода десятичной цифры необходимо получить её дополнение до старшей цифры в 10сс, которая равна девяти. Значит, в инвертированной тетраде получается значение, большее нужного на 6=0110, и его надо вычесть из псевдообратного кода. Заменяя вычитание сложением в ДК, получим корректирующий код: -610=-01102=1010дк Таким образом, для формирования обратного кода десятичного числа в коде 8-4-2-1 надо инвертировать тетрады, представляющие цифры этого числа, и прибавить потетрадно код 1010, отбрасывая единицы переноса между тетрадами. При сложении двух чисел сумма в к-ом разряде числа может быть записана формулой: Sk = Ak+Bk+Ck, где Ак,Вк- цифры в к-ом разряде слагаемых, Ск- единица переноса в к-ый разряд из предыдущего разряда. Для определения правильных корректирующих кодов при сложении необходимо проанализировать все возможные варианты формирования тетрад суммы, чтобы в необходимых случаях возникали единицы переноса в соседний старший разряд десятичного числа и тетрада суммы была верной. 1. Sk = Ak+Bk+Ck<10 – единицы переноса в старший разряд нет и коррекция не нужна; 2. 10 Признаком введения коррекции являются «неправильные» тетрады, соответствующие десятичным числам 10,11,12,13,14,15, обнаружить которые нетрудно: все они имеют единицу в старшем разряде и единицу в 3-ем или 2-ом разрядах двоичного кода. Простейшая комбинационная схема для обнаружения «неправильных» тетрад должна работать в соответствии с логическим уравнением: К1(К2 3. Sk
Поиск по сайту: |
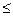 Sk
Sk 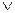 К3)=1, если в двоичной тетраде разряды обозначены так К1К2К3К4.
К3)=1, если в двоичной тетраде разряды обозначены так К1К2К3К4. 16 – единица переноса в старшую тетраду возникает естественно, однако в самой тетраде результат неверный: нужно получить (Ak+Bk+Ck-10), а получается (Ak+Bk+Ck-16). Следовательно, необходима коррекция кодом +610=01102тетрад, из которых сформировалась единица переноса.
16 – единица переноса в старшую тетраду возникает естественно, однако в самой тетраде результат неверный: нужно получить (Ak+Bk+Ck-10), а получается (Ak+Bk+Ck-16). Следовательно, необходима коррекция кодом +610=01102тетрад, из которых сформировалась единица переноса.