|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задание 6. Умножение двоично-десятичных чисел
В качестве сомножителей взять целую часть чисел А и В, представить их в коде с естественными весами и перемножить, используя два алгоритма : - старорусский метод удвоения - деления пополам; - метод десятично-двоичного разложения множителя. Результат проверить. Основные теоретические сведения Двоичная арифметика Правила перевода чисел через промежуточные системы счисления Любое смешанное число
где
Для перевода целых чисел и правильных дробей из одной позиционной СС в другую применяются различные правила. Общее правило перевода целых чисел Пусть
Разделим обе части приведенной формулы на новое основание
В правой части равенства сформировались: целая часть первого частного и первый остаток от деления Чтобы перевести целое число в новую СС, его надо последовательно делить на основание новой СС до тех пор , пока не получится частное, у которого целая часть равна «0». Число в новой СС записывается из остатков от последовательного деления, причем, последний остаток будет старшей цифрой целого числа в новой СС. Общее правило перевода правильных дробей Пусть
Умножим обе части равенства на новое основание
В правой части равенства первое слагаемое Чтобы перевести правильную дробь из одной позиционной СС в другую, её надо последовательно умножать на основание новой СС до тех пор, пока в новой дроби не будет получено требуемого количества цифр, определяемого заданной точностью. Правильная дробь в новой СС записывается из целых частей произведений, и целая часть первого произведения будет старшей цифрой новой дроби. Перевод дробей - бесконечный процесс и может быть выполнен лишь приближенно. Чтобы сохранить точность исходной дроби, надо определить требуемое количество цифр в изображении дроби по новому основанию. Если
Далее выполняется округление по последнему разряду, после чего этот последний разряд отбрасывается. При переводе неправильных дробей отдельно преобразуется целая и дробная части по сформулированным выше правилам, после чего смешанное число записывается в новой системе счисления.
Поиск по сайту: |
 в позиционной системе счисления (СС) с основанием
в позиционной системе счисления (СС) с основанием 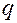 можно записать:
можно записать: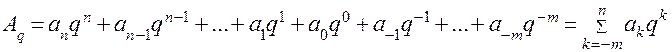
 <
<  – разрядный вес цифры
– разрядный вес цифры  – количество разрядов в целой части числа;
– количество разрядов в целой части числа;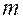 - количество разрядов в дробной части числа.
- количество разрядов в дробной части числа. - основание исходной СС,
- основание исходной СС, 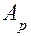 . Тогда целое число в СС с новым основанием
. Тогда целое число в СС с новым основанием 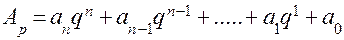 .
.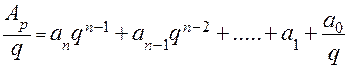
 - младшая цифра целого числа в новой СС. Далее целую часть первого частного следует разделить на новое основание
- младшая цифра целого числа в новой СС. Далее целую часть первого частного следует разделить на новое основание 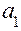 и т.д. Это позволяет сформулировать известное правило:
и т.д. Это позволяет сформулировать известное правило:
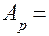
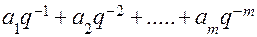

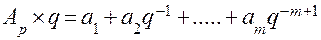
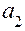 ( как целую часть второго произведения) и т.д. Отсюда следует правило:
( как целую часть второго произведения) и т.д. Отсюда следует правило: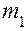 – количество цифр в исходной дроби с основанием
– количество цифр в исходной дроби с основанием  – количество цифр в дроби с новым основанием
– количество цифр в дроби с новым основанием  можно получить формулу:
можно получить формулу: