В дополнительном коде с простой коррекцией

Этот алгоритм умножения в ДК проигрывает в быстродействии алгоритму с автоматической коррекцией, но имеет определенную историческую ценность и весьма полезен в учебных целях.

В основе алгоритма – смесь принципов умножения в ПК и в ДК с обязательным введением коррекции результата, если хотя бы один из сомножителей отрицательный.

Сомножители заносятся в регистры в ДК без знака, а знаки заносятся в отдельные триггеры. Знак произведения определяется как и при умножении в ПК сложением по модулю 2 знаковых разрядов сомножителей. Модули сомножителей перемножаются по правилам умножения в ПК одним из четырех способов – получается псевдопроизведение, которое требует коррекции:

¾ если один сомножитель отрицателен, прибавляется дополнительный код от модуля положительного сомножителя;

¾ если оба сомножителя отрицательны, прибавляются дополнительные коды от модулей обоих сомножителей, то есть их прямые коды.

Алгоритм достаточно сложный и трудоемкий из-за необходимости введения коррекции. Обычно при ручном счете сначала получают псевдопроизведение, а затем выполняют коррекцию. Если в моделях реализовать этот алгоритм, то после получения псевдопроизведения необходимо иметь исходные сомножители в старших разрядах регистров для коррекции результата.

Анализ способов умножения позволяет сделать вывод, что сохранить множитель для коррекции несложно – достаточно реализовать в регистре сдвиг с перезаписью, когда разряды при сдвиге не «теряются», а заносятся в освобождающиеся разряды регистра.

На рисунке 10 приведена модель сдвигового регистра с перезаписью: при сдвиге вправо младший разряд р2 заносится на место освобождающегося старшего разряда. Аналогично реализуются и регистры с перезаписью со сдвигом влево. Таким образом в моделях множительных устройств сохраняется множитель для выполнения коррекции псевдопроизведения.

Рисунок 10 – Регистр множителя в моделях с простой коррекцией

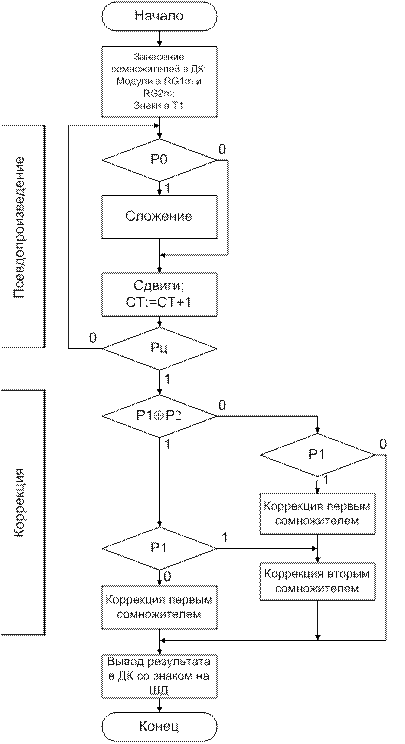
Возможность сохранить множимое в разных способах различна. В первом способе умножения n-разрядное множимое не сдвигается, и в цикле формирования псевдопроизведения поступает в старшие разряды сумматора. Это позволяет без проблем организовать коррекцию псевдопроизведения как до получения псевдопроизведения, так и после его формирования на там же оборудовании.

Во втором способе умножения множимое поступает в младшие разряды 2n-разрядного сдвигового регистра и после формирования псевдопроизведения множимое окажется в старших разрядах регистра, что и необходимо для выполнения коррекции.

В третьем способе умножения более сложная ситуация: множимое заносится в n-разрядный несдвиговый регистр, и в цикле умножения поступает в младшие разряды сумматора, а для коррекции множимое следует послать в старшие разряды. Разрешить эту ситуацию можно с помощью более сложного мультиплексора, что позволит выполнить коррекцию как до получения псевдопроизведения, так и после на том же оборудовании.

В четвертом способе умножения рекомендуется выполнить коррекцию до формирования псевдопроизведения, т.к. множимое заносится в старшие разряды 2n-разрядного сдвигового регистра, а по окончании цикла окажется в младших разрядах, что неудобно для коррекции.

Таким образом, во втором способе умножения следует выполнять коррекцию после получения псевдопроизведения, в четвертом способе – корректироватьдополучения псевдопроизведения, а в первом и третьем способах последовательность может быть любой.

Во всех моделях данного типа наряду со стандартным набором регистров, сумматора, счетчика, необходимо формировать ДК от сомножителей, для чего введены совокупности схем сложения по модулю 2 (инверсия) и предусмотрена подача управляющего сигнала на вход переноса сумматора.

Новыми в структуре рассматриваемых моделей будут мультиплексоры, предназначенные для передачи информации с нескольких источников на один приемник, которым является входное плечо сумматора.

В моделях для первого, второго и четвертого способов умножения достаточно двухплечевого мультиплексора с одним управляющим сигналом, а в модели для третьего способа умножения необходим мультиплексор с двумя управляющими сигналами.

На рисунке 11 приведена обобщенная схема алгоритма умножения в ДК с простой коррекцией, в которой выделены два блока: блок формирования псевдопроизведения и блок коррекции. Последовательность выполнения этих блоков зависит от способа умножения, что аргументировано выше.

Задача студента состоит в правильной разработке микропрограммы. При этом рекомендуется предварительно определить опытным путем, какое входное плечо мультиплексора подключается к выходу при подаче управляющих сигналов, чтобы не ошибиться при выполнении коррекции.

На рисунке 11 использованы следующие обозначения:

¾ Р0 – анализируемый разряд множителя;

¾ Р1 – знак множителя;

¾ Р2 – знак множимого;

¾ Рц – признак окончания цикла.

Рисунок 11 – Схема алгоритма умножения в ДК с простой коррекцией

Поиск по сайту: