 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Длина отрезка и ее измерение
Понятие длины отрезка и ее измерения были уже использованы неоднократно, в частности, когда рассматривали натуральное число как меру величины. В этом пункте мы только обобщим представления о длине отрезка как геометрической величине. В геометрии длина - это величина, характеризующая протяженность отрезка, а также других линий (ломаной, кривой). В нашем курсе будет рассмотрено только понятие длины отрезка. При его определении будем использовать введенное в теме 18 понятие «отрезок состоит из отрезков». Определение.Длиной отрезка называется положительная величина, обладающая следующими свойствами: 1) равные отрезки имеют равные длины; 2) если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей. Эти свойства длины отрезка используются при ее измерении. Чтобы измерить длину отрезка, нужно иметь единицу длины. В геометрии такой единицей является длина произвольного отрезка. Как показано в теме 18, результатом измерения длины отрезка является положительное действительное число - его называют численным значением длины отрезка при выбранной единице длины или мерой длины данного отрезка. Если обозначить длину отрезка буквой X, единицу длины - Е, а получаемое при измерении действительное число - буквой а, то можно записать: а=mЕ (Х) или Х = а∙Е. Получаемое при измерении длины отрезка положительное действительное число должно удовлетворять ряду требований: 1. Если два отрезка равны, то численные значения их длин тоже равны. 2. Если отрезок х состоит из отрезков х1 и х2, то численное значение его длины равно сумме численных значений длин отрезков х1 и х2. 3. При замене единицы длины численное значение длины данного отрезка увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой. 4. Численное значение длины единичного отрезка равно единице. Доказано, что положительное действительное число, являющееся мерой длины заданного отрезка, всегда существует и единственно. Доказано также, что для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом. Заметим, что часто, ради краткости речи, численное значение длины отрезка называют просто длиной. Например, в задании «Найдите длину данного отрезка» под словом «длина» подразумевается численное значение длины отрезка. Не менее часто допускают и другую вольность - говорят: «Измерь отрезок» вместо «Измерь длину отрезка». Задача. Построить отрезок, длина которого 3,2Е. Каким будет численное значение длины этого отрезка, если единицу длины Е увеличить в 3 раза ? Решение. Построим произвольный отрезок и будем считать его единичным. Затем построим прямую, отметим на ней точку А и отложим от нее 3 отрезка, длины которых равны Е. Получим отрезок АВ, длина которого 3Е (рис. 1).
Чтобы получить отрезок длиной 3,2Е, надо ввести новую единицу длины. Для этого единичный отрезок надо разбить либо на 10 равных частей, либо на 5, поскольку 0,2 = Чтобы выполнить второе требование задачи, воспользуемся свойством 3, согласно которому при увеличении единицы длины в 3 раза численное значение длины данного отрезка уменьшается в 3 раза. Разделим 3,2 на 3, получим: 3,2 : 3 == 3
Поиск по сайту: |
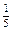. Если от точки В отложить отрезок, равный 
= 1 
. Таким образом, при единице длины 3Е численное значение длины построенного отрезка АС будет равно 1