 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ТЕМА 19. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ И ИХ СВОЙСТВА
Содержание 1. Понятие геометрической фигуры. 2. Углы. 3. Параллельные и перпендикулярные прямые. 4. Треугольники. 5. Четырехугольники. 6. Многоугольники. 7. Окружность и круг. 8. Построение геометрических фигур на плоскости. 9. Преобразования геометрических фигур. Понятие преобразования Основная литература [4, 5, 13, 14, 15, 28, 29, 34]; Дополнительная литература [13, 49, 51, 65, 68, 75, 76, 78, 85] Понятие геометрической фигуры Геометрическую фигуру определяют как любое множество точек. Отрезок, прямая, круг, шар - геометрические фигуры. Если все точки геометрической фигуры принадлежат одной плоскости, она называется плоской. Например, отрезок, прямоугольник - это плоские фигуры. Существуют фигуры, не являющиеся плоскими. Это, например, куб, шар, пирамида. Так как понятие геометрической фигуры определено через понятие множества, то можно говорить о том, что одна фигура включена в другую (или содержится в другой), можно рассматривать объединение, пересечение и разность фигур. Например, объединением двух лучей АВ и МК (рис. 1) является прямая КВ, а их пересечение есть отрезок АМ. К А М В
Рис. 1 Различают выпуклые и невыпуклые фигуры. Фигура называется выпуклой, если она вместе с любыми двумя своими точками содержит также соединяющий их отрезок. Фигура F1, изображенная на рисунке 2, выпуклая, а фигура F2 - невыпуклая.
F2 X
Y
Для многоугольников известно другое определение: многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей его сторону. Так как равносильность этого определения и данного выше для многоугольника доказана, то можно пользоваться и тем, и другим. Основываясь на этих понятиях, рассмотрим другие геометрические фигуры, изучаемые в школьном курсе планиметрии. Рассмотрим их определения и основные свойства, принимая их без доказательства. Знание этого материала и умение применять к решению несложных геометрических задач является той основой, на которой можно строить методику обучения младших школьников элементам геометрии. Углы Напомним, что угол - это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало - его вершиной. Угол обозначают по-разному: указывают либо его вершину, либо его стороны, либо три точки: вершину и две точки на сторонах угла: Ð А, Ð (k, l), Ð АВС. Угол называется развернутым, если его стороны лежат на одной прямой. Угол, составляющий половину развернутого угла, называется прямым. Угол, меньший прямого, называется острым. Угол, больший прямого, но меньший развернутого, называется тупым. Кроме понятия угла, данного выше, в геометрии рассматривают понятие плоского угла. Плоский угол - это часть плоскости, ограниченная двумя различными лучами, исходящими из одной точки. Углы, которые рассматривают в планиметрии, не превосходят развернутого. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми. Сумма смежных углов равна 180°. Справедливость этого свойства вытекает из определения смежных углов.
Поиск по сайту: |
Выпуклыми фигурами являются плоскость, прямая, луч, отрезок, точка. Нетрудно убедиться в том, что выпуклой фигурой является круг (рис. 3). Если продолжить отрезок XY до пересечения с окружностью, то получим хорду АВ. Так как хорда содержится в круге, то отрезок XY тоже содержится в круге и, значит, круг - выпуклая фигура.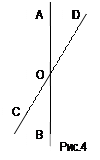
Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. Углы АОВ и СОВ, а также углы АОС и D0В - вертикальные (рис. 4).