 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вертикальные углы равны
Справедливость этого свойства вытекает из определения вертикальных углов и свойства смежных углов. Параллельные и перпендикулярные прямые Определение.Две прямые на плоскости называются параллельными, если они не пересекаются. Если прямая а параллельная прямой b, то пишут а || b. Рассмотрим некоторые свойства параллельных прямых, и прежде всего признаки параллельности. Признаками называют теоремы, в которых устанавливается наличие какого-либо свойства объекта, находящегося в определенной ситуации. В частности, необходимость рассмотрения признаков параллельности прямых вызвана тем, что нередко в практике требуется решить вопрос о взаимном расположении двух прямых, но в то же время нельзя непосредственно воспользоваться определением. Рассмотрим следующие признаки параллельности прямых: 1.Две прямые, параллельные третьей, параллельны друг другу. 2.Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны. Справедливо утверждение, обратное второму признаку параллельности прямых: если две параллельные прямые пересечены третьей, то внутренние накрест лежащие углы равны, а сумма односторонних углов равна 180°. Важное свойство параллельных прямых раскрывается в теореме, носящей имя древнегреческого математика Фалеса: если параллельные прямые, пересекающие стороны угла отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне. Определение. Две прямые называются перпендикулярными, если они пересекаются под прямым углом. Если прямая а перпендикулярна прямой b, то пишут а ± b. Основные свойства перпендикулярных прямых нашли отражение в двух теоремах: 1. Через каждую точку прямой можно провести перпендикулярную к ней прямую, и только одну. 2. Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, имеющий концом их точку пересечения. Конец этого отрезка называется основанием перпендикуляра. Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой. Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой. Треугольники Треугольник - одна из простейших геометрических фигур. Но его изучение породило целую науку - тригонометрию, которая возникла из практических потребностей при измерении земельных участков, составлении карт местности, конструировании различных механизмов. Первые упоминания о треугольнике и его свойствах содержатся в египетских папирусах. Например, в них предлагается находить площадь равнобедренного треугольника как произведение половины основания на боковую сторону, хотя для любого равнобедренного треугольника с малым углом при вершине, противоположной основанию, такой способ дает приближенное значение площади. Многие свойства треугольников были открыты и доказаны математиками Древней Греции. Среди них - знаменитая теорема Пифагора. Рассмотрим основные понятия, связанные с треугольником. Треугольником называется геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков. Любой треугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из треугольника и его внутренней области, также называют треугольником (или плоским треугольником). В любом треугольнике выделяют следующие элементы: стороны, углы, высоты, биссектрисы, медианы, средние линии. Углом треугольника АВС при вершине А называется угол, образованный полупрямыми АВ и АС. Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, содержащей противолежащую сторону. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне. Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Треугольники называются равными, если у них соответствующие стороны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон. На практике и в теоретических построениях часто пользуются признаками равенства треугольников, обеспечивающими более быстрое решение вопроса об отношениях между ними. Таких признаков три. 1. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 2. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. 3. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны. Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми, а третья сторона называется основанием треугольника. Равнобедренные треугольники обладают рядом свойств, например: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. Отметим еще несколько важных свойств треугольников. 1. Сумма углов треугольника равна 180°.Из этого свойства следует, что в любом треугольнике хотя бы два угла острые. 2. Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине. 3. В любом треугольнике каждая сторона меньше суммы двух других сторон. Для прямоугольного треугольника с углом 30° справедливо следующее свойство: катет, противолежащий этому углу, равен половине гипотенузы. Для прямоугольного треугольника верна теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Четырехугольники Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков, причем никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника, а соединяющие их отрезки - его сторонами. Любой четырехугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из четырехугольника и его внутренней области, также называют четырехугольником (или плоским четырехугольником). Вершины четырехугольника называют соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями. Стороны четырехугольника, исходящие из одной вершины, называются соседними. Стороны, не имеющие общего конца, называются противолежащими. У четырехугольника АВСD (рис. 5) вершины А и В - соседние, а вершины А и С - противолежащие; стороны АВ и ВС - соседние, ВС и АD -противолежащие; отрезки АС и ВD -диагонали данного четырехугольника.
Поиск по сайту: |
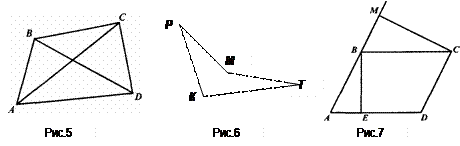Четырехугольники бывают выпуклые и невыпуклые. Так, четырехугольник АВСD (рис. 5) - выпуклый, а четырехугольник КРМТ (рис. 6) невыпуклый. Среди выпуклых четырехугольников выделяют параллелограммы и трапеции.