 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Все элементарные функции непрерывны в каждой точке области определения
Определения. Точка Если в точке Разность Если в точке Если в точке
то точка Решение задачи IV типового варианта Пример 20. Исследовать данную функцию на непрерывность и построить ее график:
▲ Функция Для точки
Замечание. Символ
т. е. функция Скачок
Скачок
–2 –1 O 1 x
Рис.1 График данной функции Решение задачи V типового варианта Пример 21. Исследовать функцию ▲ Для точки
т. е. в точке Для точки
Итак,
Знания и умения, которыми должен владеть студент Знания на уровне понятий, определений, описаний, формулировок Множество. Элементы теории доказательств. 1.1. Классификация числовых множеств. Операции над множествами. 1.2. Точная верхняя и точная нижняя границы ограниченных числовых множеств. 1.3. Свойства множества вещественных чисел. 1.4. Абсолютная величина вещественного числа. Свойства. 1.5. Высказывание. Логические связки. Кванторы. 1.6. Необходимые и достаточные условия. Прямая и обратная теоремы. Функции. 2.1. Функция как отображение множеств. 2.2. Функция числового аргумента. 2.3. Числовая последовательность. 2.4. Классификация функций. 2.5. Сложная функция. 2.6. Обратная функция; ее свойства. 2.7. Элементарные функции. Предел. 3.1. Предел числовой последовательности. 3.2. Определение предела функции. 3.3. Бесконечно малые функции (бмф) и бесконечно большие функции (ббф). 3.4. Сравнение бмф и ббф. 3.5. Таблица эквивалентных бесконечно малых функций. Непрерывность. 4.1. Непрерывность функции в точке и на промежутке. 4.2. Свойства непрерывных функций. 4.3. Точки разрыва и их классификация.
Поиск по сайту: |
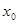 называется точкой разрыва функции
называется точкой разрыва функции  , если в ней не выполняются условия непрерывности.
, если в ней не выполняются условия непрерывности.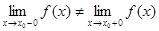 , то точка
, то точка 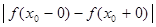 называется скачком функции
называется скачком функции 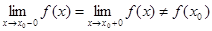
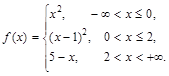
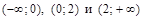 , где она задана непрерывными элементарными функциями. Следовательно, разрыв возможен только в точках
, где она задана непрерывными элементарными функциями. Следовательно, разрыв возможен только в точках 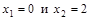 .
.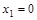 имеем:
имеем: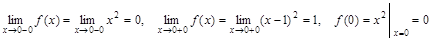 .
. позволяет выбрать нужное аналитическое выражение для функции
позволяет выбрать нужное аналитическое выражение для функции 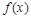 из уравнений, ее определяющих.
из уравнений, ее определяющих.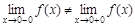 ,
,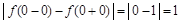 .
. Для точки
Для точки  находим:
находим: .
. ,
, т. е. в точке
т. е. в точке 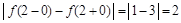 .
.
 y
y


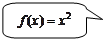

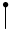

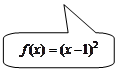
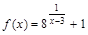 на непрерывность в точках
на непрерывность в точках  .
.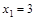 имеем:
имеем: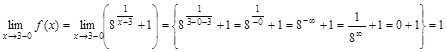 ,
,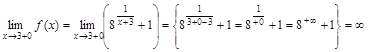 ,
,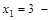 точка разрыва второго рода).
точка разрыва второго рода). имеем:
имеем: ,
, 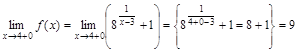 ,
, 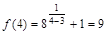 .
. предел слева равен пределу справа и равен значению функции в точке. Функция
предел слева равен пределу справа и равен значению функции в точке. Функция 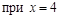 . ▼
. ▼