 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоретические сведенияСтр 1 из 7Следующая ⇒
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ ФУНКЦИИ. ПРЕДЕЛЫ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Р Г Г М У
Санкт-Петербург Одобрено Научно-методическим советом РГГМУ УДК 51 Веретенников В. Н. Учебно-методическое пособие для выполнения индивидуального задания. Функции. Пределы. Непрерывность функции. – СПб.: Изд. РГГМУ. 2006. – 24 с.
Активизация познавательной деятельности студентов, выработка у них способности самостоятельно решать достаточно сложные проблемы может быть достигнута при такой организации учебного процесса, когда каждому студенту выдаются индивидуальные домашние задания (ИДЗ) с обязательным последующим контролем их выполнения и выставлением оценок. Предлагаемое пособие адресовано преподавателям и студентам и предназначено для проведения практических занятий и самостоятельных (контрольных) работ в аудитории и выдачи ИДЗ.
© Веретенников В. Н. © Российский государственный гидрометеорологический университет (РГГМУ), 2006.
ПРЕДИСЛОВИЕ
"Математика" является не только мощным средством решения прикладных гидрометеорологических задач, но также и элементом общей культуры. Именно в рамках математического образования студент получает навыки творческого подхода к решению интеллектуальных проблем, точному пониманию средств возможностей решения проблем, знакомится с современными информационными технологиями. Целью математического образования является: 1. Воспитание достаточно высокой математической культуры. 2. Привитие навыков современных видов математического мышления. 3. Привитие навыков использования математических методов и основ математического моделирования в практической деятельности. Воспитание у студентов математической культуры включает в себя ясное понимание необходимости математической составляющей в общей подготовке студента. Он должен выработать представление о роли и месте математики в современной цивилизации и в мировой культуре, уметь логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений. В пособии приведены основные теоретические сведения, отражающие базисные понятия по разделу "Функции. Пределы. Непрерывность функции"; базисные методы решения основных задач; приведен перечень знаний, умений и навыков, которыми должен владеть студент; указана используемая литература.
ЧИСЛОВЫЕ МНОЖЕСТВА Основные теоретические сведения Математические теории, как правило, находят свой выход в том, что позволяют перерабатывать один набор чисел (исходные данные) в другой набор чисел, составляющих промежуточную или окончательную цель вычислений. По этой причине особое место в математике и ее приложениях занимают числовые функции (точнее, так называемые дифференцируемые числовые функции). Ни составляют главный объект исследования классического анализа. Но сколь-нибудь полное с точки зрения современной математики описание свойств этих функций невозможно без точного определения множества вещественных чисел, на котором эти функции действуют. Определение. Множество Rназывается множеством действительных (вещественных) чисел, а его элементы – действительными (вещественными) числами, если выполнен следующий комплекс условий, называемый аксиоматикой вещественных чисел: аксиомы сложения, аксиомы умножения, связь сложения и умножения, аксиомы порядка, связь сложения и порядка вR, связь умножения и порядка R, аксиома полноты (непрерывности). Вещественные числа можно изображать точками на координатной прямой. Поэтому множество всех вещественных чисел называют числовой прямой, а сами числа – точками, и при рассмотрении числовых множеств часто пользуются их геометрической интерпретацией. Будем использовать следующие обозначения и терминологию: N – множество всех натуральных чисел; Z– множество всех целых чисел;
отрезок, интервал, полуинтервал, полупрямую и числовую прямую будем называть также промежутком; окрестность точки
Абсолютная величина Определение. Модулем (абсолютной величиной) вещественного числа
Абсолютные величины обладают следующими свойствами:
Поиск по сайту: |



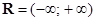 – множество всех вещественных чисел (числовая прямая);
– множество всех вещественных чисел (числовая прямая);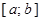 – сегмент (отрезок)–множество всех вещественных чисел
– сегмент (отрезок)–множество всех вещественных чисел , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 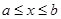 ;
;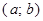 – интервал –множество всех вещественных чисел
– интервал –множество всех вещественных чисел 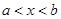 ;
;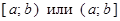 – полуинтервал (полусегмент) –множество всех вещественных чисел
– полуинтервал (полусегмент) –множество всех вещественных чисел  ;
;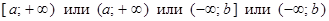 – полупрямая –множество всех вещественных чисел
– полупрямая –множество всех вещественных чисел 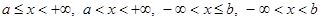 ;
;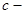 любой интервал, содержащий точку
любой интервал, содержащий точку  ;
;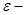 окрестность точки
окрестность точки  .
.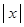 , определяемое равенством:
, определяемое равенством: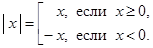
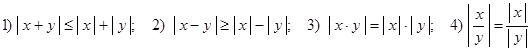 .
.