 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Бесконечно малые и бесконечно большие последовательности
Определение. Последовательность
Определение. Последовательность Обозначение: Если при этом, начиная с некоторого номера все члены бесконечно большой последовательности положительны (отрицательны), то пишут С геометрической точки зрения это означает, что в любой (сколь угодно большой) окрестности нуля находится лишь конечное число членов последовательности, а вне ее – бесконечно много членов. Отметим, что бесконечно большая последовательность не является сходящейся и символическая запись Всякая бесконечно большая последовательность является неограниченной, поскольку вне любой окрестности нуля имеется член последовательности (даже все члены последовательности начиная с некоторого номера). Обратное утверждение неверно: неограниченная последовательность может и не быть бесконечно большой. Теорема 3. Алгебраическая сумма конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью. Теорема 4. Произведение бесконечно малой последовательности на ограниченную величину является бесконечно малой последовательностью. Следствие. Произведение конечного числа бесконечно малых есть бесконечно малая. Теорема 5. Если последовательность Решение задачи 1 типового варианта Пример 1. Доказать, что ▲В соответствии с определением предела последовательности (стр. 5) зададим произвольно сколь угодно малое число
Для отыскания числа
то от этого неравенства переходим к неравенству
Из последнего неравенства следует, что
Следовательно, Таким образом, при произвольном числе Придавая
Следовательно, начиная с номера Пример 2. Дана последовательность ▲ В соответствии с определением предела последовательности (стр. 5) зададим произвольно сколь угодно малое число
Решим неравенство
Следовательно,
Поиск по сайту: |
 называется бесконечно малой, если
называется бесконечно малой, если 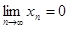 .
. такое, что
такое, что 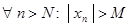 .
. .
. .
.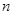 , определена последовательность
, определена последовательность  , которая является бесконечно малой. Если последовательность
, которая является бесконечно малой. Если последовательность 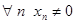 , то последовательность
, то последовательность  (указать
(указать  ).
). и покажем, что для него можно найти такое число
и покажем, что для него можно найти такое число  будет выполняться неравенство
будет выполняться неравенство .
.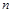 . Так как
. Так как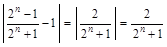 ,
, .
. можно принять число, удовлетворяющее условию
можно принять число, удовлетворяющее условию .
. , где
, где  – целая часть числа
– целая часть числа 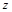 .
. – предел рассматриваемой последовательности.
– предел рассматриваемой последовательности. конкретное значение в правой части неравенства
конкретное значение в правой части неравенства  , можно указать соответствующий номер, начиная с которого все члены последовательности будут находиться в
, можно указать соответствующий номер, начиная с которого все члены последовательности будут находиться в  точки
точки  , то
, то и
и  .
.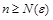 , т. е.
, т. е.  ,
,  . ▼
. ▼ . Доказать, что ее предел
. Доказать, что ее предел  .
. .
. .
.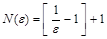 . Таким образом, существует число
. Таким образом, существует число  . ▼
. ▼