 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
Начало изучению понятия предела числовой последовательности положено уже в элементарной математике. Примерами таких последовательностей могут служить: последовательность всех членов арифметической и геометрической последовательностей; последовательность периметров правильных n – угольников, вписанных в данную окружность; последовательность Определение 1. Если каждому числу по некоторому закону поставлено в соответствие вещественное число Другими словами, числовую последовательность можно определить как множество пар чисел Числа Символ Сокращенно последовательность Последовательности могут быть заданы посредством описания их словами или формулой ее общего члена. При любом способе задания последовательности каждый ее член определяется номером занимаемого места. Поэтому возможно такое определение последовательности. Определение 2. Функция Значения По самому определению, последовательность содержит бесконечное число элементов: любые два ее элемента отличаются, по крайней мере, своими номерами. Геометрически последовательность изображается на координатной прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности. Последовательности Определение. Последовательность
С геометрической точки зрения это означает, что все члены последовательности находятся в некоторой окрестности Определение. Последовательность
Определение. Число Обозначение:
Поиск по сайту: |
 приближенных значений
приближенных значений  .
.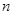 из натурального ряда чисел
из натурального ряда чисел 
 , то множество вещественных чисел
, то множество вещественных чисел  называется числовой последовательностью или просто последовательностью.
называется числовой последовательностью или просто последовательностью. , в которых первое число принимает последовательно значения
, в которых первое число принимает последовательно значения  последовательности; а число
последовательности; а число  .
. , областью определения которой является множество натуральных чисел, называется последовательностью.
, областью определения которой является множество натуральных чисел, называется последовательностью. функции
функции  . Саму последовательность
. Саму последовательность  называются соответственно суммой, разностью, произведением и частным двух последовательностей:
называются соответственно суммой, разностью, произведением и частным двух последовательностей:  (для частного
(для частного 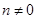 ).
). такое, что
такое, что  .
. точки
точки  .
. .
. называется пределом последовательности
называется пределом последовательности 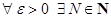 такой, что
такой, что  выполняется неравенство
выполняется неравенство 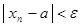 .
. .
.