 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Умножить числитель и знаменатель на выражения, сопряженные числителю и знаменателю
2) После этого сделать необходимые упрощения (приведение подобных членов, сокращение, выделение критического множителя и т. д.) и перейти к пределу. Решение задачи 6 типового варианта Пример 3. Найти указанный предел ▲
Пример 4. Найти указанный предел ▲
Пример 5. Найти указанный предел ▲
Раскрытие неопределенностей Для того чтобы раскрыть неопределенность вида С помощью алгебраических и тригонометрических преобразований разложить числитель и знаменатель на множители, выделив критический множитель. Для нахождения предела использовать первый замечательный предел
Решение задачи 9 типового варианта Пример 6. Найти ▲ Пример 7. Найти ▲
▲ Следует запомнить, что Пример 8. Найти ▲ Пример 9. Найти ▲ Пример 10. Найти ▲ Пример 11. Найти ▲
Пример 11. Найти ▲ Если под знаком предела делается замена переменной, то Все величины, входящие под знак предела, должны быть выражены через эту новую переменную, А из равенства, выражающего зависимость между старой переменной и новой, должен быть определен предел новой переменной. Пример 12. Найти ▲
Раскрытие неопределенностей вида Если предел отношения двух алгебраических функций нужно числитель и знаменатель дроби поделить на старшую степень переменной Или в числителе и знаменателе вынести множитель, переменную
Решение задачи 3-5 типового варианта Пример 13. Найти ▲
Пример 14. Найти ▲
Пример 15. Найти ▲ Такие примеры можно решать и устно, пользуясь следующим правилом: Предел отношения двух алгебраических функций 1) отношению коэффициентов перед старшей степенью 2) нулю, если степень алгебраической функции в числителе меньше степени алгебраической функции в знаменателе; 3) Неопределенность При отыскании пределов вида
Раскрытие неопределенности Неопределенность вида
Способ «подгонки» состоит в следующем: функцию Показатель степени И тогда
Решение задачи 7-8 типового варианта Пример 16. Найти ▲
Пример 17. Найти ▲
Поиск по сайту: |
 .
.


 . ▼
. ▼ .
.
 . ▼
. ▼ .
.


 . ▼
. ▼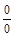 .
.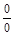 при отыскании предела дроби, содержащей тригонометрические функции в случае, когда предел и числителя, и знаменателя дроби равен нулю, надо
при отыскании предела дроби, содержащей тригонометрические функции в случае, когда предел и числителя, и знаменателя дроби равен нулю, надо .
. .
. . ▼
. ▼ .
.
 ▼
▼ .
. .
. . ▼
. ▼ .
. . ▼
. ▼ .
. . ▼
. ▼ .
.

 . ▼
. ▼ .
. . ▼
. ▼ .
.

 . ▼
. ▼ .
. дает неопределенность вида
дает неопределенность вида  , встречающуюся в членах этой дроби.
, встречающуюся в членах этой дроби. , где
, где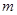 – старшая степень переменной.
– старшая степень переменной. .
.
 . ▼
. ▼ .
.
 . ▼
. ▼ .
.
 . ▼
. ▼ , если степень алгебраической функции в числителе больше степени алгебраической функции в знаменателе.
, если степень алгебраической функции в числителе больше степени алгебраической функции в знаменателе. . Условия, при которых возникает эта неопределенность, связана с пределом
. Условия, при которых возникает эта неопределенность, связана с пределом  .
. , имеет место формула
, имеет место формула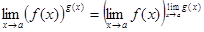 .
. .
. представляют в виде
представляют в виде  .
. записывают в виде:
записывают в виде:  ,
, .
. .
.

 . ▼
. ▼ .
. . ▼
. ▼