 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предельный переход и арифметические операции
Теорема 1. Пусть функции 1) 2) 3) Следствие 1. Постоянный множитель можно выносить за знак предела:
Следствие 2. Если Следствие 3 (Предел целой рациональной функции). Если
т. е. при отыскании предела целой рациональной функции можно в аналитическом выражении функции заменить аргумент его предельным значением. Следствие 4 (Предел дробно-рациональной функции). Если
то т. е. при отыскании предела дробно-рациональной функции можно в аналитическом выражении функции заменить аргумент его предельным значением, если при этом предельном значении знаменатель не обращается в нуль. Предел элементарной функции в точке ее определения равен частному значению функции в этой точке: Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям вида Отметим также, что
Раскрытие неопределенностей Для того чтобы раскрыть неопределенность вида 1) определить тип неопределенности, 2) если неопределенность вида Замечание. Двучлен Решение задачи 1-2 типового варианта Пример 1. Найти указанный предел ▲
Замечание. Многочлены, стоящие в числителе и знаменателе, обращаются в нуль
Пример 2. Найти указанный предел ▲
Раскрытие неопределенностей Для того чтобы раскрыть неопределенность вида
Поиск по сайту: |
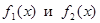 определены в некоторой окрестности точки
определены в некоторой окрестности точки 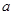 , быть может, кроме самой точки
, быть может, кроме самой точки 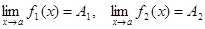 , то
, то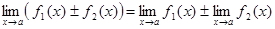 ;
;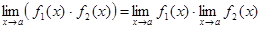 ;
; .
.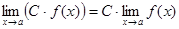 .
.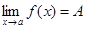 и
и  – натуральное число, то
– натуральное число, то  .
.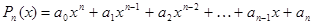 , то
, то 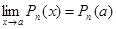 ,
,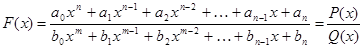 ,
,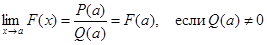 ,
,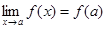 .
.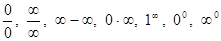 .
.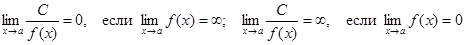 ;
;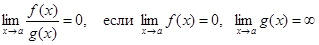 ;
;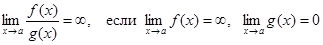 .
.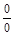 .
.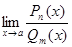 , нужно
, нужно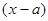 .
.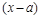 в дальнейшем будем называть «критическим множителем»
в дальнейшем будем называть «критическим множителем»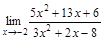 .
.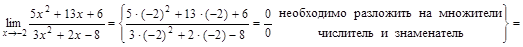
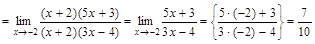 . ▼
. ▼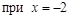 . Если
. Если 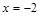 – корень многочлена, то этот многочлен делится
– корень многочлена, то этот многочлен делится 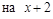 без остатка. По теореме Безу в этом случае каждый многочлен (в числителе и знаменателе) может быть представлен в виде произведения критического множителя
без остатка. По теореме Безу в этом случае каждый многочлен (в числителе и знаменателе) может быть представлен в виде произведения критического множителя 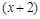 на некоторый многочлен. Таким образом, нахождение предела сводится, прежде всего, к выделению в числителе и знаменателе критического множителя
на некоторый многочлен. Таким образом, нахождение предела сводится, прежде всего, к выделению в числителе и знаменателе критического множителя 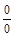 . Для разложения на множители можно воспользоваться теоремой Виета, или использовать деление «уголком» на «критический множитель»:
. Для разложения на множители можно воспользоваться теоремой Виета, или использовать деление «уголком» на «критический множитель»: 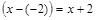 .
.
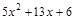
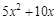
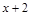
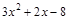
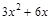
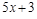
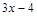


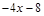
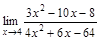
 . ▼
. ▼