 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дисперсия альтернативного признака.
Среди варьирующих признаков, которые изучает статистика, встречаются признаки вариации, которые проявляются в том, что у одних единиц совокупности они встречаются, у других нет. Признаки, которыми обладают данные единицы и не обладают другие, называются альтернативными. Количественно вариация альтернативного признака в численности всей совокупности обозначается
Среднее значение альтернативного признака равно доле, которая является обобщающей характеристикой совокупности по этому варьирующему признаку:
Тогда дисперсия альтернативного признака равна:
Таким образом, дисперсия альтернативного признака равна произведению доли на дополняющее эту долю до единицы число. Т.к.,
Приемы анализа вариационных рядов. Закономерные изменения частот за счет изменения варьирующего признака в вариационных рядах называется закономерностями распределения. Главной задачей анализа вариационных рядов является выявление закономерностей распределения и характера распределения. Например, распределение рабочих по уровню заработной платы зависит от условий: - квалификации; - нормы выработки; - расценок; - условий труда – это общее условие. Тип закономерности распределения – это отражение в вариационных рядах общих условий, определяющих распределение в однородной совокупности. Общие условия, определяющие тип закономерностей, познаются анализом сущности явления тех его свойств и условий, которые определяют изменчивость вариационного признака. Следовательно, должна быть построена кривая распределения. Кривая распределения – это графическое изображение частот варьирующего ряда в виде непрерывной линии, где частоты связаны с вариантами функционально. Существует теоретическая кривая распределения и фактическая. Теоретическая кривая выражает общую закономерность данного распределения в чистом виде исключающую влияния случайных условий.
Рис. 4. Полигон распределения
Полигон распределения – непрерывная линия, характеризующая фактическую кривую распределения, поскольку в нем отражаются как общие, так и случайные условия, определяющие распределение. В статистике наиболее часто для сопоставления фактических и теоретических кривых используют нормальный тип распределения, который имеет следующее уравнение:
где В экономической статистике кривая нормального распределения (рис. 5) встречается достаточно редко, но нормальное распределение может служить моделью для выяснения степени и характера отклонения от нее фактического распределения.
Рис. 5. Кривая нормального распределения
Выравнивание фактического распределения по кривой нормального распределения.
Cостоит из нескольких этапов: - сравнивают фактические и теоретические частоты. По фактическим данным определяют теоретические частоты кривой нормального распределения, которая является функцией нормированного отклонения; - проверяют на сколько распределение признака соответствует нормальному.
Рис. 6. Кривые фактического и нормального распределения
Критерии согласия. Математическая статистика дает несколько показателей, по которым можно судить, на сколько фактическое распределение согласуется с нормальным. Эти показатели называются критериисогласия. Критерий согласия Колмагорова (критерий
n – число наблюдений. По приведенному примеру критерий По специальной таблице вероятности для критерия согласия
Поиск по сайту: |
 а доля единиц, не обладающих признаком, обозначается
а доля единиц, не обладающих признаком, обозначается  и принимает значения
и принимает значения  , тогда:
, тогда: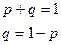


 , то средний квадрат отклонений не может быть больше 0,25.
, то средний квадрат отклонений не может быть больше 0,25.

 - ордината кривой нормального распределения /частость/,
- ордината кривой нормального распределения /частость/,  - это нормированное распределение
- это нормированное распределение 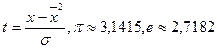 .
.







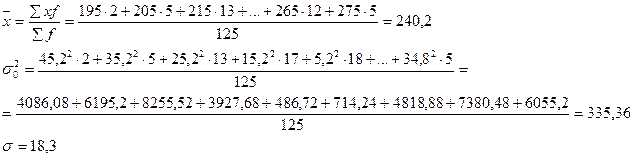
 ;
;  постоянное число 68,30
постоянное число 68,30
 ) определяется путем деления max разности коммулятивных частот на корень квадратный из числа наблюдений:
) определяется путем деления max разности коммулятивных частот на корень квадратный из числа наблюдений: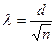 , где d – максимальное отклонение фактической частоты от фактической частоты;
, где d – максимальное отклонение фактической частоты от фактической частоты;