 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Закон сложения дисперсии.
Если статистическая совокупность разбита на несколько групп по одинаковому признаку, то средняя величина и дисперсия могут быть определены не только для всей совокупности, но и для отдельной ее части. В зависимости от этого можно выделить межгрупповую и внутригрупповую вариацию. А, следовательно, рассчитать среднюю величину и дисперсию, как межгрупповую, так и внутригрупповую. В зависимости от всех условий в совокупности определяют общую дисперсию, которая зависит от этих условий:
где Межгрупповаядисперсия отражает вариацию признака изучаемой совокупности, изменение признака которой возникает под влиянием фактора, положенного в основу группировки. Межгрупповая дисперсия характеризует колеблимость групповых средних около общей средней:
где
Средняя внутригрупповая дисперсия характеризует случайную вариацию в каждой отдельной группе. Данная вариация возникает в зависимости от влияния других факторов, которые не учитываются при группировке.
Между общей дисперсией и средней из групповой дисперсии и межгрупповой существует взаимосвязь:
Свойства дисперсии. 1. Если из всех значений вариант вычесть какое-то постоянное число, то средний квадрат отклонений не изменится:
2. Если все значения вариант разделить на какое-то постоянное число, то средний квадрат отклонений уменьшиться в а раз:
3. Если средний квадрат отклонений от любой величины а – которая отличается от средней арифметической х, то он будет всегда больше среднего квадрата отклонений от средней арифметической:
используя 2-ое свойство дисперсии в математической статистике можно рассчитать дисперсию способом моментов. Средний квадрат отклонений от средней величины имеет свойства min, т.е. дисперсия от средней всегда меньше дисперсий исчисляемых от других величин. В этом случае, если а – постоянное число = 0, то, следовательно, средний квадрат отклонений будет определяться по формуле:
Значит, средний квадрат отклонений
Также способ моментов называется способом отсчета от условного нуля. Данный способ можно применять только в тех случаях, если в вариационных интервальных рядах интервалы одинаковы. Используя 2-ое свойство дисперсии, разделив все варианты на величину интервала, получим формулу дисперсии:
где i – величина интервала для данной совокупности Пример. Рассчитать все показатели вариации, доказать закон сложения дисперсии.
Общая дисперсия
В среднем по региону средний объем товарной продукции равен 18,14 млрд. руб.
Ср. квадратное отклонение АО:
Расчет межгрупповой дисперсии
Если разделить дисперсию групповых средних на общую дисперсию, то получим коэффициентдетерминации.
Поиск по сайту: |
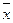- общее среднее для всей изучаемой совокупности, т.е. среднее для всех групп, входящих в совокупность.
- средняя величина признака по относительным группам;
- частота отдельных групп.
– закон сложения дисперсии
, но больше на определенную величину, а эта величина определена, как квадрат разности между средней и этой, условно взятой величиной:
- ср. квадрат значений признака;
- квадрат среднего значения признака.
равен разности между средним квадратом значения признака и квадратом ср. значения признака.
; 
, 
по региону средний объем товарной продукции в регионе АО 16,82
, 
Закон сложения дисперсии доказан.
- дает эмпирическое корреляционное отношение, показывает тесноту между группировочным признаком и результативным.