 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дифракционная решетка как спектральный прибор. Угловая и линейная дисперсия. Разрешающая способность.
Как видно из
Обычно спектрографы с дифракционной решеткой работают при m = 1 или 2, очень редко при m = 3. Качество решетки как спектрального прибора может быть охарактеризовано рядом параметров. К ним относятся угловая дисперсия, дисперсионная область и разрешающая способность. 3. 7. Дисперсия и разрешающая сила спектрального прибора. @
 , где dl - расстояние между спектральными линиями, а dλ – разность длин волн этих линий. Определение справедливо также для разности частот линий dν. Угловая дисперсия  , где dφ – разность углов между лучами, отличающимися на dλ или dν соответственно. На рис. 3.9 показаны два луча, идущие под углами φ и φ + dφ, и имеющие длины волн λ и λ + dλ, соответственно.
Для определения угловой дисперсии дифракционной решетки продифференцируем условие главного максимума dsinφ = mλ. Мы получим dcosφ dφ = mdλ, откуда следует
Разрешающей способностью спектрального прибора принято называть отношение
где
Так как спектральные линии, изображенные на рис. 3.4, некогерентны, результирующая интенсивность равна сумме интенсивностей (сплошная кривая на рис. 3.4). Наличие провала в центре кривой распределения интенсивности указывает на условный характер критерия Рэлея. Для разрешающей способности дифракционной решетки легко получить из выражения (3.3):
Поиск по сайту: |
положение узких главных максимумов зависит от длины волны 
. Это позволяет использовать решетку в качестве спектрального прибора. Решетка способна разлагать свет в спектр. Для этого могут быть использованы дифракционные максимумы различных порядков (кроме m = 0). Практически, однако, используются главные максимумы, расположенные в пределах основного лепестка диаграммы излучения одиночной щели, имеющего полуширину 
. Отсюда можно получить оценку:
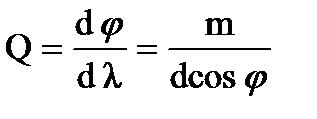. При малых углах cosφ≈1 и Q ≈ ≈m/d, т.е. чем выше порядок спектра и меньше период решетки, тем больше угловая дисперсия. Она не зависит от числа щелей в решетке и характеризует степень растянутости спектра в области данной длины волны.
– минимальный интервал между двумя близкими спектральными линиями, при котором они могут быть разрешены, то есть отделены одна от другой. В качестве критерия разрешения используется обычно критерий разрешения Рэлея. Спектральные линии с близкими значениями 
считаются разрешенными, если главный максимум дифракционной картины для одной спектральной линии совпадает по своему положению с первым дифракционным минимумом для другой спектральной линии. Рис. 3.4. поясняет критерий Рэлея.
