Дифракция рентгеновских лучей на пространственной решетке кристаллов. Формула Вульфа- Брегга. Изучение структуры кристаллов.

Поскольку рентгеновские лучи обладают высокой проникающей способностью, отраженная их часть составляет ничтожную долю лучей, прошедших в кристалл. Однако при условии ин­терференционного максимума лучей, отраженных от разных плоскостей кристалла, можно добиться их значительного усиле­ния.

Разобьем кри­сталл на ряд парал­лельных плоскостей, про­ходящих через узлы кристаллической решетки и отстоящих друг от друга на рас­стояние d (рис. 3.8). Пусть на кристалл па­дает плоская монохроматическая волна рентгеновского излуче­ния под углом скольжения θ (угол между направлением падаю­щего луча и кристаллографической плоскостью). Рассмотрим лучи 1’ и 2’, отразившиеся от атомов А и В двух параллельных плоскостей I и II соответственно. Абсолютный показатель пре­ломления любых сред для рентгеновских лучей близок к еди­нице, поэтому отраженные лучи 1’ и 2’ по закону отражения выйдут из кристалла под тем же углом θ к плоскостям I и II. Лучи 1’ и 2’ когерентны и будут интерферировать между собой, подобно лучам, идущим от соседних щелей дифракционной ре­шетки. Для определения разности хода лучей 1’ и 2’ из точки А опустим перпендикуляры на лучи 2 и 2’ (на рис. 3.8 это пунктир­ные линии). Искомая разность хода Δ = 2 dsinθ. Лучи будут уси­ливать друг друга при 2 dsinθ = = mλ, где m = 1,2…. – порядок дифракционного максимума. Данное соотношение называется формулой Вульфа-Брэгга. Если известна длина волны рентгеновских лучей, то по виду дифракционной картины можно определить структуру кристалла. На этом основан метод изучения структуры веще­ства, получивший название рентгеноструктурного анализа.

Интерференционные максимумы должны удовлетворять условию Вульфа–Брэггов:

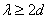, (m = 1, 2, 3, ... .).(9.5.1)Из формулы (9.5.1) видно, что дифракция будет наблюдаться лишь при . Т. е. при условии будут отсутствовать дифракционные максимумы. Поэтому условие называют условием оптической однородности кристалла.Из (9.5.1) следует, что наблюдение дифракционных максим+умов возможно только при определенных соотношениях между λ и θ. Этот результат лежит в основе спектрального анализа рентгеновского излучения, так как длину волны определяют по известным d, m и измеренному на опыте углу.

Поиск по сайту: