|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Раздел 8. Многокритериальная оптимизации сложных объектов ⇐ ПредыдущаяСтр 9 из 9
На рис. 8.1 приведено непрерывное замкнутое множество допустимых вариантов сложного объекта с одинаковыми значениями технических характеристик, различающихся cтоимостью изготовления Си и интенсивностью отказов Λ
Рис.8.1 Множество допустимых вариантов сложного объекта На рис. 8.2 приведено множество эффективных вариантов сложного объекта с минимальной cтоимостью изготовления Си min (Λ), зависящей от значения интенсивности его отказа Λ.
Рис.8.2 Парето-множество эффективных вариантов сложного объекта На рис. 8.3 представлено множество эффективных вариантов сложного объекта, для которых определены их стоимости эксплуатации Сэ (Λ) за весь срок их использования . На рис. 8.4 представлена зависимость суммарных затрат (Си + Сэ) на изготовление и эксплуатацию эффективных вариантов объекта от значения их интенсивности отказов Λ, минимальное значение этих затрат и соответствующий ему оптимальный вариант объекта с оптимальной стоимостью изготовления Сиopt и оптимальной интенсивностью его отказа Λopt. На рис. 8.5 представлена структурная схема объекта А0, состоящего из одной сборки А12 и компонента А3. Сборка А12 состоит из компонентов А1 и А2. Для каждого из компонентов А1, А2 и А3 можно определить эффективные варианты их исполнения, но невозможно определить зависимость стоимости их эксплуатации Сэ(Λ) от интенсивности отказов, поскольку каждый компонент – не автономен и по отдельности не может эксплуатироваться. Составной объект А0 - автономен. Поэтому он может автономно эксплуатироваться и для него можно определить зависимость стоимости
. Рис. 8.3 Стоимость эксплуатации эффективных вариантов объекта
Рис. 8.4 Оптимальный вариант объекта с минимальными суммарными затратами (Си+Сэ)min
Рис. 8.5 Постановка задачи оптимизации составного объекта эксплуатации Сэ(Λ) от интенсивности отказов. Для определения оптимального варианта объекта А0 необходимо найти его эффективные варианты, то есть получить зависимость минимальной стоимости его изготовления Сиmin(Λ) от интенсивности его отказов. Поскольку стоимость и интенсивность отказов нескольких компонентов складываются из стоимостей и интенсивностей отказов каждого компонента, то для определения эффективных вариантов объектов А12 и А0 из эффективных вариантов компонентов А1, А2 и А3 можно воспользоваться аппаратом динамического программирования [11]. Сначала определяются эффективные варианты объекта А12 по эффективным вариантам компонентов А1 и А2. Затем можно определить эффективные варианты объекта А0 по эффективным вариантам объекта А12 и компонента А3. Для эффективных вариантов объекта А0 известна зависимость минимальной стоимости его изготовления Сиmin(Λ) от интенсивности его отказов. Складывая эту зависимость с функцией стоимости эксплуатации Сэ(Λ) этих же вариантов, можно определить оптимальный эффективный вариант объекта А0opt и соответствующий ему оптимальные значения стоимости изготовления Cиopt, эксплуатации Cэopt и интенсивности отказов Λopt. На рис. 8.6 представлены эффективные варианты сканера, принтера и монитора
Рис. 8.6 Эффективные варианты трёх компонентов
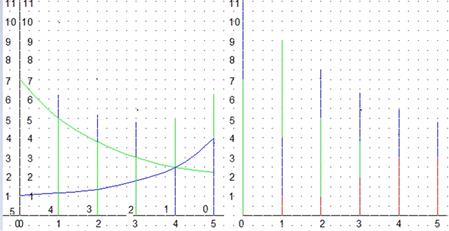
На рис. 8.7 представлено графическое построение методом динамического программирования эффективного варианта безотказной пары из сканера и принтера. На рис. 8.8 представлено графическое построение методом динамического программирования эффективного варианта одноотказной пары из сканера и принтера. На рис. 8.9 представлено графическое построение методом динамического программирования эффективного варианта двухотказной пары из сканера и принтера
Рис. 8.7 Эффективный вариант безотказной пары сканер-принтер
Рис. 8.8 Эффективный вариант одноотказной пары сканер-принтер .
Рис. 8.9 Эффективный вариант двухотказной пары сканер-принтер На рис. 8.10 представлено графическое построение методом динамического программирования эффективного варианта трёхотказной пары из сканера и принтера. На рис. 8.11 представлено графическое построение методом динамического программирования эффективного варианта четырёхотказной пары из сканера и принтера.
Рис. 8.10 Эффективный вариант трёхотказной пары сканер-принтер
Рис. 8.11 Эффективный вариант четырёхотказной пары сканер-принтер
Рис. 8.12 Эффективный вариант пятиотказной пары сканер-принтер На рис. 8.12 представлено графическое построение методом динамического программирования эффективного варианта пятиотказной пары из сканера и принтера. Зная эффективные варианты пары сканер-принтер и эффективные варианты монитора можно аналогично определить эффективные варианты тройки сканер-принтер-монитор. Предлагается выполнить построение для тройки компонентов по представленному выше алгоритму самостоятельно. На рис. 8.13 представлен окончательный результат – оптимальные устройства УВВ по критерию минимальных затрат на изготовление и эксплуатацию.
Рис. 8.13 Оптимальные эффективные варианты устройств ввода-вывода (УВВ)
Пример определения оптимальных вариантов комплектующих ПК На рис. 8.14 представлен состав персонального компьютера с известными ценами новых (безотказных за три года) комплектующих для него и ценами бывших в употреблении (БУ) (семиотказных за три года) комплектующих. Цены указаны в тысячах рублей. В последнем столбце указана стоимость ремонта нового компьютера и компьютера, состоящего из БУ комплектующих.
Рис. 8.14 Исходные данные для определения оптимальных комплектующих ПК
На рис. 8.15 - 8.17 показан способ заполнения цен комплектующих для промежуточных значений отказа во всех строках таблицы по закону геометрической прогрессии.
Рис. 8.15 Заполнение строк таблицы числами по закону прогрессии
Рис. 8.16 Выбор геометрической прогрессии
Рис. 8.17 Результат заполнения таблицы ценами комплектующих ПК На рис. 8.18 и 8.19 показана проверка правильности заполнения столбцов. На рис. 8.20 и 8.21 показана вставка пустого столбца для построения эффективных вариантов разноотказных пар сканер-принтер. На рис. 8.21 - 8.28 представлена процедура ввода формул для определения эффективных вариантов разноотказных пар сканер-принтер от безотказной до семиотказной.
Рис. 8.18 Проверки правильности заполнения цен в столбцах сканера и ремонта
Рис. 8.19 Проверки правильности заполнения цен в столбцах сканера и ремонта
Рис. 8.20 Вставка пустого столбца для построения эффективных пар сканер-принтер
Рис. 8.21 Ввод формулы для эффективной безотказной пары сканер-принтер
Рис. 8.22 Ввод формулы для эффективной одноотказной пары сканер-принтер
Рис. 8.23 Ввод формулы для эффективной двухотказной пары сканер-принтер На рис. 8.29 и 8.30 показана проверка правильности введённых формул для определения эффективных разноотказных пар сканер-принтер. На рис. 8.31 - 8.33 представлена вставка пустого столбца для копирования в него формул по определению эффективных пар сканер-принтер.
Рис. 8.24 Ввод формулы для эффективной трёхотказной пары сканер-принтер
Рис. 8.25 Ввод формулы для эффективной четырёхотказной пары сканер-принтер
Рис. 8.26 Ввод формулы для эффективной пятиотказной пары сканер-принтер На рис. 8.34 - 8.36 представлено копирование эффективных пар сканер-принтер в столбец УВВ для получения эффективной тройки её комплектующих и проверка
Рис. 8.27 Ввод формулы для эффективной шестиотказной пары сканер-принтер
Рис. 8.28 Ввод формулы для эффективной семиотказной пары сканер-принтер
Рис. 8.29 Настройка проверки правильности вычисления эффективных пар сканер-принтер
Рис. 8.30 Проверка правильности вычисления эффективных пар сканер-принтер
Рис. 8.31 Выбор столбца для вставки пустого
Рис. 8.32 Вставка пустого столбца
Рис. 8.33 Ввод названия УВВ для пустого столбца
Рис. 8.34 Копирование формул столбца сканер-принтер и вставка их в столбец УВВ
Рис. 8.35 Выделение столбцов для УВВ правильности расчёта. На рис. 8.37 – 8.38 показано копирование формульных значений цен для эффективных вариантов тройки комплектующих УВВ в численные значения в этот же столбец, но ниже. Это нужно для получения
Рис. 8.36 Проверка правильности вычисления эффективных компонентов УВВ
Рис. 8.37 Копирование значений эффективных УВВ в отдельный столбец
Рис. 8.38 Вставка значений эффективных УВВ в отдельный столбец
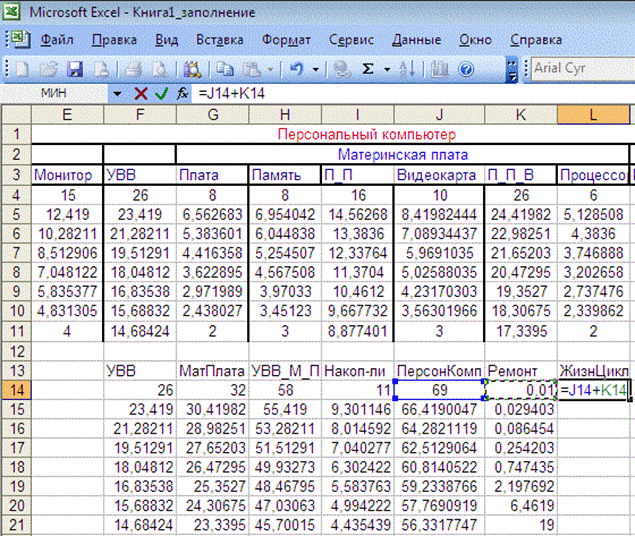
Рис. 8.39 Вставка значений эффективных комплектующих и блоков персонального компьютера
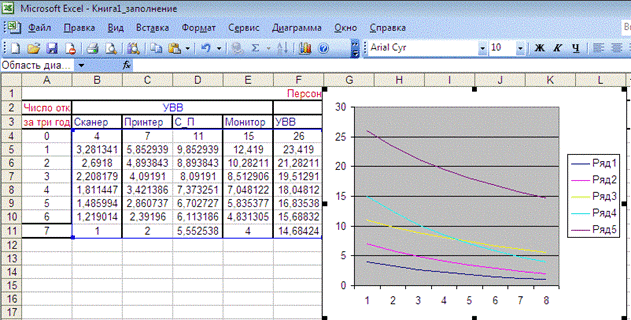
Рис. 8.40 Суммарные затраты на изготовление и эксплуатацию безотказного компьютера эффективных вариантов частей компьютера на уровне блоков. На рис. 8.39 показаны эффективные варианты УВВ, материнской платы, накопителей и всего компьютера в виде формул и в виде числовых значений. На рис. 8.40 – 8.43 пока-
Рис. 8.41 Суммарные затраты на изготовление и эксплуатации всех вариантов компьютера
Рис. 8.42 Выделение столбцов изготовления, ремонта и суммарных затрат компьютера
Рис. 8.43 Определение оптимального компьютера, ремонта и минимальных затрат
Рис. 8.44 Определение оптимальных накопителей и остальной части компьютера
Рис. 8.45 Определение оптимальных вариантов материнской платы и УВВ
Рис. 8.46 Определение оптимальных вариантов материнской платы и УВВ зано вычисление суммарных затрат на изготовление и ремонт разноотказных компьютеров, а также определение оптимального компьютера с минимальными суммарными затратами. На рис. 8.44-8.51 представлен процесс определения опти
Рис. 8.47 Определение оптимальных вариантов комплектующих накопителей
Рис. 8.48 Оптимальные варианты процессора и остальных комплектующих материнской платы
Рис. 8.49 Определение оптимальных вариантов всех комплектующих материнской платы
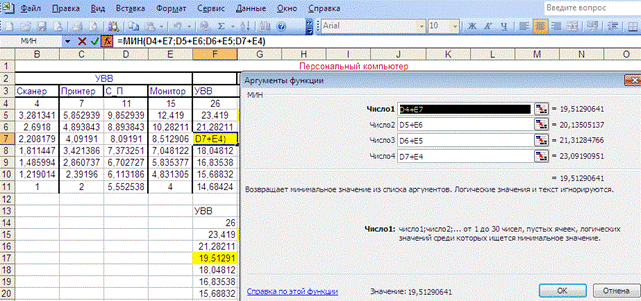
Рис. 8.50 Определение оптимальных вариантов комплектующих УВВ
Рис. 8.51 Оптимальные варианты всех комплектующих персонального компьютера
мальных комплектующих на основе известных оптимальных вариантов блоков компьютера: накопителей, материнской платы и УВВ.
Варианты заданий многокритериальной оптимизации сложного объекта
01. Максимальное число отказов за пять лет 5
02. Максимальное число отказов за пять лет 6
03. Максимальное число отказов за пять лет 7
04. Максимальное число отказов за пять лет 5
05 Максимальное число отказов за пять лет 6
06. Максимальное число отказов за пять лет 7
07. Максимальное число отказов за пять лет 5
08. Максимальное число отказов за пять лет 6
09. Максимальное число отказов за пять лет 7
10. Максимальное число отказов за пять лет 5
11. Максимальное число отказов за пять лет 6
12. Максимальное число отказов за пять лет 7
13. Максимальное число отказов за пять лет 5
14. Максимальное число отказов за пять лет 6
15. Максимальное число отказов за пять лет 7
16. Максимальное число отказов за пять лет 5
17. Максимальное число отказов за пять лет 6
18. Максимальное число отказов за пять лет 7
19. Максимальное число отказов за пять лет 5
20. Максимальное число отказов за пять лет 6
21. Максимальное число отказов за пять лет 7
22. Максимальное число отказов за пять лет 5
23. Максимальное число отказов за пять лет 6
24. Максимальное число отказов за пять лет 7
25. Максимальное число отказов за пять лет 5
26. Максимальное число отказов за пять лет 6
27. Максимальное число отказов за пять лет 7
28. Максимальное число отказов за пять лет 5
29. Максимальное число отказов за пять лет 6
30. Максимальное число отказов за пять лет 7
31. Максимальное число отказов за пять лет 5
32. Максимальное число отказов за пять лет 6
33. Максимальное число отказов за пять лет 7
34. Максимальное число отказов за пять лет 5
35. Максимальное число отказов за пять лет 6
36. Максимальное число отказов за пять лет 7
37. Максимальное число отказов за пять лет 5
38. Максимальное число отказов за пять лет 6
39. Максимальное число отказов за пять лет 7
40. Максимальное число отказов за пять лет 5
41. Максимальное число отказов за пять лет 6
42. Максимальное число отказов за пять лет 7
43. Максимальное число отказов за пять лет 5
44. Максимальное число отказов за пять лет 6
45. Максимальное число отказов за пять лет 7
46. Максимальное число отказов за пять лет 5
47. Максимальное число отказов за пять лет 6
48. Максимальное число отказов за пять лет 7
49. Максимальное число отказов за пять лет 5
50 Максимальное число отказов за пять лет 6
51. Максимальное число отказов за пять лет 7
52. Максимальное число отказов за пять лет 5
Библиографический список 1. Лебедев А.А. Введение в анализ и синтез систем. Учебное пособие. - М. Машиностроение. 2001. -351 с. 2. Данилов Н.Н. Введение в математическую экономику. Новосибирск, 2004. -431 с. 3. Методы оптимизации в примерах и задачах / Авторы: Бирюков Р.С., Городецкий С.Ю., Григорьева С.А.и др. Учебно-методическое пособие. - Нижний Новгород: Нижегородский госуниверситет, 2010. - 101 с. 4. Гайкович А.И. Основы теории проектирования сложных технических систем СПб.: Моринтех, 2001. – 432 с. 5. Сергиенко И.В. Математические модели и методы решения задач дискретной оптимизации. Киев: Наукова Думка, 1988 - 472 с. 6. Зеленский, В. А. Проектирование сложных систем. Электрон. учеб. пособие / В. А. Зеленский; Минобрнауки России. Самар.гос.аэрокосм. ун-т им. С.П.Королева Самара 2012. – 96 с. 7. Афанасьева О.В., Голик Е.С., Первухин Д.А. Теория и практика моделирования сложных систем: Учеб. пособие. – СПб: СЗТУ, 2005 –131 с.Печерских И.А. Математические модели в экономике: Учебное пособие / И.А. Печерских, А.Г. Семёнов; КТИПП. – Кемерово, 2011. – 191 с. 8. Ковалёв М.Я. Модели и методы календарного планирования. Курс лекций. Минск, БГУ, 2004. – 63с. 9. Вагнер Г. Основы исследования операций. Том 2. –М., Мир, 1973. – 488 с. 10. А.В. Лотов, И.И. Поспелова Многокритериальные задачи принятия решений. Учебное пособие. – М.: МАКС Пресс, 2008. – 197 с. 11. Беллман Р. Динамическое программирование. М.: ИИЛ, 1960. – 400 с. 12. Смирнов О.Л. Автоматизация технологического проектирования: Учеб. пособие / СПб ГУАП, СПб., 2001. -66с.
СОДЕРЖАНИЕ Предисловие……………………………………………………….……………….….3 1. Составление математических моделей……………………..………………………..3 2. Задачи безусловной оптимизации……………………..……………………………22 3. Задачи условной оптимизации……………………………………………………....26 4. Оптимизация задач линейного программирования ……………………….………30 5. Целочисленное решение задач линейного программирования …………..………61 6. Оптимизация задач методом ветвей и границ……………………………….…….67 7. Оптимизация линейных задач с бинарными переменными……………………….85 8. Многокритериальная оптимизации сложных объектов ……………..……………94 Библиографический список…………………………………………………...……119
Поиск по сайту: |