 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Раздел 2. Задачи безусловной оптимизации
Замкнутое и одновременно ограниченное множество в метрическом пространстве (в пространстве Rn с заданным на нем понятием расстояния) называется компактным. Компактное множество Функция f дважды дифференцируема, если для всех i,j=1,…,n существуют частные производные от частных производных, то есть
Симметричная относительно диагонали nxn- матрица
Оптимальным решением задач (2.1) называется пара (x*,f (x*)), где x* - точка максимума (минимума), а f(x*)- значение функции f в этой точке, то есть ее максимальное (минимальное) значение на множестве Х. Решение задачи (2.1) требует разрешения трех проблем: 1) проблему существования оптимального решения; 2) проблему установления необходимых и достаточных признаков оптимальности (то есть характерных свойств, присущих точкам максимума и минимума); 3) проблему численного вычисления оптимальных решений. В задачах (2.1) применяются экстремальные точки двух видов: локальный максимум (минимум) и глобальный максимум (минимум). Точка f(x0) ≥ f(x) (f(x0) ≤f(x)) для всех Теорема (Вейерштрасса). Для того, чтобы в задаче (2.1) существовала точка глобального максимума (минимума), достаточно, чтобы допустимое множество X было компактно в Rn, а целевая функция f непрерывна на X. Следствие (теоремы Вейерштрасса). Если функция f непрерывна на Rn и
то f достигает своего глобального минимума в любом замкнутом подмножестве X пространства Rn. Признаки оптимальности приведем в случае, когда в (2.1)X
и называются задачами безусловной оптимизации. Чтобы точка
Все точки x0, удовлетворяющие условию (2.3) , называются стационарными точками (точки подозрительные на экстремум). Чтобы x0 была точкой локального максимума (минимума) в задаче (2.2) необходимо и достаточно, чтобы
для всех Известно, что дважды дифференцируемая на выпуклом множестве Х функция f вогнута (выпукла) тогда и только тогда, когда для любых векторов
для всех k =1,…,n. Здесь символом
где Если в (2.5) неравенства строгие, то получаем необходимое и достаточное условие отрицательной (положительной) определенности матрицы Гессе в точке x0 . Условие (2.5) называется критерием Сильвестра для знакоопределенных матриц. Поскольку условия (2.4) труднопроверяемы, то при проверке необходимых условий оптимальности в задачах (2.2) применяют критерий Сильвестра. Следовательно, при помощи условий (2.3) - (2.5) можно предложить следующий алгоритм решения задач (2.2) : вычислить все стационарные точки (найти все решения уравнения (2.3) ); выяснить характер экстремума стационарных точек (с использованием условий (2.4) - (2.5) ), для чего применить критерий Сильвестра; среди всех точек локального максимума (минимума) найти точки глобального максимума (минимума), сравнивая значение функции f в этих точках.
Пример решения Определить максимальное значение функции двух переменных и оптимальные значения переменных f(x,y) = x3 + y2 – 6xy - 39x + 18y +100 Берём производные по переменным, приравниваем их значения нулю и решаем систему
fx' = 3x2 - 6y - 39 = 0; fy' = 2y - 6x + 18 = 0;
x2 - 2y - 13 = x2 - (3x - 18) - 13 = x2 - 3x + 5 = 0 x1 = 1, y1 = -6; x2 = 5, y2 = 6; A = fxx'' = 6x; B = fyy” = 2; C = fxy” = -6;
Если A*B – C2 < 0 , то анализируемая точка - точка перегиба. Если A*B – C2 > 0 и А > 0, то в анализируемой точке функция минимальна. Если A*B – C2 > 0 и А < 0, а B > 0, то в анализируемой точке функция максимальна. В примере точка М = (1, -6) - точка перегиба, так как A*B - C2 = 6*1*2 - 36 < 0; а точка М = (5, 6) - точка минимума, так как A*B – C2 = 6*5*2 - 36 > 0;
Варианты заданий 1 2x3 + 2y2 – 9xy - 27x + 12y +100 2 x3 + 3y2 – 6xy - 28x + 21y +150 3 2 x3 + 4y2 – 9xy - 21x + 18y +100 4 x3 + 5y2 – 6xy - 39x + 21y +150 5 x3 + 2y2 – 9xy - 27x + 12y +100 6 2x3 + y2 – 9xy - 29x + 21y +150 7 x3 + 2y2 – 6xy - 21x + 18y +100 8 2x3 + y2 – 6xy - 39x + 12y +100 9 x3 + y2 – 9xy - 27x + 18y +150 10 2x3 + y2 – 6xy - 21x + 21y +100 11 x3 +2 y2 – 9xy - 39x + 18y +100 12 2x3 + y2 – 9xy - 27x + 21y +150 13 x3 + y2 – 6xy - 21x + 18y +100 14 2x3 + 2y2 – 9xy - 27x + 21y +100 15 x3 + 2y2 – 6xy - 39x + 18y +100 16 2x3 + y2 – 9xy - 21x + 21y +150 17 x3 + 2y2 – 6xy - 27x + 18y +100 18 x3 + 2y2 – 9xy - 27x + 18y +100 19 2x3 + y2 – 6xy - 39x + 21y +150 20 x3 + 2y2 – 9xy - 39x + 18y +100 21 x3 + 2y2 – 6xy - 27x + 21y +150 22 2x3 + y2 – 9xy - 27x + 18y +100 23 x3 + 2y2 – 6xy - 39x + 21y +100 24 2x3 + 3y2 – 6xy - 39x + 21y +150 25 x3 + 4y2 – 7xy - 39x + 21y +200 26 x3 + 2y2 – 8xy - 39x + 21y +100 27 2x3 + 2y2 – 9xy - 39x + 21y +150 28 x3 + 3y2 – 7xy - 39x + 21y +200 29 2x3 + 2y2 – 9xy - 39x + 21y +100 30 x3 + 2y2 – 6xy - 39x + 21y +150 31 x3 + 2y2 – 6xy - 39x + 21y +200 32 x3 + 2y2 – 6xy - 39x + 21y +100 33 x3 + 2y2 – 6xy - 39x + 21y +150 34 x3 + 4y2 – 8xy - 39x + 21y +200 35 2x3 + y2 – 6xy - 39x + 21y +100 36 x3 + 2y2 – 6xy - 39x + 21y +150 37 x3 + 3y2 – 9xy - 39x + 21y +200 38 2x3 + 4y2 – 6xy - 39x + 21y +100 39 x3 + 5y2 – 6xy - 39x + 21y +150 40 x3 + 6y2 – 6xy - 39x + 21y +200 41 x3 + 5y2 – 9xy - 39x + 21y +100 42 2x3 + 4y2 – 6xy - 39x + 21y +150 43 x3 + 6y2 – 9xy - 39x + 21y +200 44 2x3 + 6y2 – 6xy - 39x + 21y +100 45 x3 + 6y2 – 9xy - 39x + 21y +150 46 x3 + 4y2 – 6xy - 39x + 21y +200 47 x3 + 3y2 – 6xy - 39x + 21y +100 48 2x3 + 6y2 – 9xy - 39x + 21y +150 49 x3 + 6y2 – 6xy - 39x + 21y +200 50 2x3 + 5y2 – 9xy - 39x + 21y +100 51 x3 + 6y2 – 6xy - 39x + 21y +150 52 x3 + 4y2 – 9xy - 39x + 21y +200
Поиск по сайту: |
 называется выпуклым, если для любых
называется выпуклым, если для любых 
 , 0 ≤ a ≤ 1. То есть выпуклое множество В кроме всех своих точек содержит и все их выпуклые комбинации. Это означает, что вместе с допустимыми x1 и x2 допустимы и их смеси. Гладкой называется функция, которая в области своего определения имеет производные, то есть является дифференцируемой.
, 0 ≤ a ≤ 1. То есть выпуклое множество В кроме всех своих точек содержит и все их выпуклые комбинации. Это означает, что вместе с допустимыми x1 и x2 допустимы и их смеси. Гладкой называется функция, которая в области своего определения имеет производные, то есть является дифференцируемой.

 называется матрицей Гессе. Задача нахождения максимального или минимального значения заданной функции на заданном множестве называется экстремальной. Имеется два вида экстремальных задач - задача на максимум и задача на минимум. Символически они записываются так:
называется матрицей Гессе. Задача нахождения максимального или минимального значения заданной функции на заданном множестве называется экстремальной. Имеется два вида экстремальных задач - задача на максимум и задача на минимум. Символически они записываются так: (2.1)
(2.1) называется точкой локального максимума (минимума), если
называется точкой локального максимума (минимума), если , где
, где  - ε-окрестность точки x0. Точка
- ε-окрестность точки x0. Точка  . Достаточное условие существования оптимальных решений задач (2.1) содержится в следующем утверждении.
. Достаточное условие существования оптимальных решений задач (2.1) содержится в следующем утверждении.
 . В этом случае задачи (2.1) принимают вид:
. В этом случае задачи (2.1) принимают вид: (2.2)
(2.2) была точкой локального экстремума в задачах (2.2) необходимо, чтобы
была точкой локального экстремума в задачах (2.2) необходимо, чтобы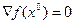 (2.3)
(2.3)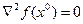 и
и 
 (2.4)
(2.4) . Здесь
. Здесь  матрица Гессе функции f в точке x0 , а
матрица Гессе функции f в точке x0 , а  - скалярное произведение.
- скалярное произведение. будет отрицательно (положительно) полуопределенной в точке x0 , если
будет отрицательно (положительно) полуопределенной в точке x0 , если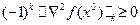
 (2.5)
(2.5) обозначен минор k-го порядка матрицы
обозначен минор k-го порядка матрицы 
 - определитель порядка k * k, вычисляемый в точке x0 .
- определитель порядка k * k, вычисляемый в точке x0 .