 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Составить модель. Описать методику решения. Привести и решить пример.
На предприятии производятся два вида продукции из двух видов сырья. Производство единицы продукта №1 (первого вида) приносит предприятию доход, равный 10 единицам, а производство единицы продукта №2 (второго вида) - доход в 8 единиц. Переработка сырья производится аппаратами двух типов, которые условно называются в дальнейшем машинами и агрегатами. На переработке сырья первого вида занято пять машин, причем производственные условия не допускают, чтобы суммарное время использования машин на этой работе превышало 40 ч (за некоторый период). На переработке сырья второго вида занято 25 машин. Суммарное время их использования в течение того же периода не должно превышать 200 ч. При производстве единицы продукта №1 на переработку сырья первого вида затрачивается 4 ч и на переработку сырья второго вида - 9 ч, в то время как производство единицы продукта №2 требует затраты 3 ч на переработку каждого из видов сырья.
Промышленная фирма производит изделие, представляющее собой сборку из трех различных узлов. Эти узлы изготовляются на двух заводах. Из-за различий в составе технологического оборудования производительность заводов по выпуску каждого из трех видов узлов неодинакова. В приводимой ниже таблице 1.1 содержатся исходные данные, характеризующие как производительность заводов по выпуску каждого из узлов, так и максимальный суммарный ресурс времени, которым в течение недели располагает каждый из заводов для производства этих узлов. Идеальной является такая ситуация, когда производственные мощности обоих заводов используются таким образом, что в итоге обеспечивается выпуск
Таблица 1.1
одинакового количества каждого из видов узлов. Однако этого трудно добиться из-за различий в производительности заводов. Более реальная цель состоит в том, чтобы максимизировать выпуск изделий, что, по существу, эквивалентно минимизации дисбаланса, возникающего вследствие некомплектности поставки по одному или двум видам узлов. Возможный объем производства каждого из трех видов узлов зависит от того, какой фонд времени выделяет каждый завод для их изготовления.
Экономика представлена двумя отраслями народного хозяйства, каждая из которых выпускает свою продукцию и затрачивает на воспроизводство труд, средства труда и предметы труда. Валовый продукт каждой отрасли за год распределяется соответственно на конечный продукт и производственное потребление, причем в процессе производства данной отрасли может применяться продукция обеих отраслей. Известно, что потребление одной отраслью продукции другой пропорционально объему валового выпуска первой из них. Конечный продукт обеих отраслей делится на валовые капитальные вложения и непроизводственное потребление. Без учета амортизационных отчислений, можно считать, что валовые капитальные вложения из одной отрасли в другую каждый год пропорциональны приросту валовой продукции второй отрасли. Определить, как должна функционировать рассматриваемая экономическая система во времени Фирма А производит некоторый товар, который имеет спрос в течение n единиц времени. Этот товар поступает на рынок в момент i (i=1,...,n). Для конкурентной борьбы с фирмой А дочерняя фирма В концерна Д, не заботясь о собственных доходах, производит аналогичный товар, который поступает на рынок в момент j (j=1,...,n). Ее цель - разорение первой фирмы, после чего ей будет легко, опираясь на капитал D, наверстать упущенное. Для этой цели проще всего продавать товары по пониженной цене. Однако имеются законы (соглашения), запрещающие поступать подобным образом. В этом случае единственным законным инструментом этой фирмы является выбор момента поступления товара на рынок. Будем считать, что качество конкурирующих товаров зависит от времени их поступления на рынок относительно друг друга - чем позднее товар выбрасывается на рынок, тем качество его выше, а реализуется только товар высшего качества. Каждая фирма должна заранее готовить свое производство к выпуску и продаже товара в выбранный период времени. А чтобы разорить первую фирму, вторая фирма должна минимизировать ее доходы
Для обеспечения нормальной работы оборудования необходимо закупить n видов запасных частей на сумму d рублей. Стоимость j-ой детали равна bj, потребность в ней есть случайная величина yj, имеющая показательный закон распределения с параметром aj. Использование j-ой детали позволяет получить прибыль cj. Отсутствие детали в случае необходимости приводит к убыткам rj. Если деталь не используется в данном периоде, то убыток составляет qj. Как распределить имеющиеся средства, чтобы общая прибыль была наибольшей?
Фабрика производит два вида лака для наружных и внутренних работ. Используется два исходных продукта: нефть и кислота. Максимально возможные суточные запасы этих продуктов определяются емкостями их хранения и равны 6 и 8 т. соответственно. Для производства 1 т. лака для внутренних работ расходуется 1 т. нефти и 2 т. кислоты. Для производства 1 т. лака для наружных работ расходуется 2 т. нефти и 1 т. кислоты. Суточный спрос на лак для наружных работ не превышает 2 т. Спрос на лак для внутренних работ – неограничен. Доход от реализации 1 т. лака для внутренних работ равен 3 миллиона рублей, а доход от реализации 1 т. лака для наружных работ - 2 миллиона рублей. Необходимо определить, какое количество лака каждого вида должна производить фабрика в сутки, чтобы доход от его реализации был максимальным.
Автотранспортная компания для перевозки грузов располагает четырьмя автомашинами следующей грузоподъемности: машина 1 - 2 т, машина 2 и машина 3 - по 5 т, машина 4 - 8 т. Для каждой автомашины известна стоимость её эксплуатации за день: для машины 1 - 15 единиц, для машины 2 - 20 единиц, для машины 3 - 19 единиц, для машины 4 - 30 единиц. Необходимо в течение одного дня развести грузы четырем получателям. В книжный магазин нужно доставить груз весом в 1 т, в мебельный магазин - в 3 т, в фермерское хозяйство - в 5 т и на сталелитейный завод - в 8 т. Одна и та же машина не может доставлять груз в книжный или мебельный магазин и на ферму. Требуется так назначить автомашины для доставки всех грузов, чтобы суммарные затраты были минимальными.
На местности имеется сеть дорог, связывающих несколько населенных пунктов. Путешественник находится в пункте a0, из которого, двигаясь по одной из трех дорог, можно попасть в пункты a1, a2, a3. Из каждого пункта опять выходят ровно три дороги, ведущие в a4, a5, a6. Из них - в a7, a8, a9 и так далее, вплоть до конечных пунктов b1 = a3*n -2, b2 = a3•n-1, b3= a3•n. Длины всех дорог заданы. Найти наиболее короткий путь из a0 в один из конечных пунктов. Решить задачу при N = 5. Оцените количество операций сложения и сравнения при ее решении по методу Беллмана, а также при полном переборе всех путей.
Построить расписаниеобслуживания n = 5 требований одним прибором, минимизирующее максимальное отклонение моментов завершения обслуживания требований от директивных сроков Lmax = maxj{Cj —dj}. Отношения предшествования заданы в виде 1 —> 2 —> 3 и 4 —> 5. Длительность обслуживания любого требования равна 2. Директивные сроки d1 = 4, d2 = 2, d3 = 4, d4 = 7, d5 = 5.
Построить математическую модель задачи о диете. Доступны следующие продукты: пирожные, 30с за шт., котлеты . 40с за шт., кола, 80c за бут., бигмаки, 70c за шт. В единице продукта содержится следующее количество приведенных ниже веществ (Таблица 1.2). Таблица 1.2
Заданы ограничения на потребление веществ в день. Сумма калорий ≥ 500 и ≤ 900. Сумма витаминов ≥ 6 . Сумма сахара ≥ 10 и ≤ 40. Сумма жира ≥ 8 и ≤ 15. Требуется определить набор из указанных продуктов на день минимальной стоимости при выполнении приведенных ограничений. Банк собирается выдать кредитов на сумму, не превышающую 10 млн $. Типы кредитов и информация о доходах по ним и рисках приведены в таблице 1.3. Банк обязан разместить ≥ 30% всех кредитов на нужды с/х и бизнеса, и ≥ 40% от кредитов на личные нужды, авто и жильё - на жильё. Общая доля невозврата по всем кредитам не должна превосходить 0.09. Необходимо определить суммы кредитов по указанным видам так, чтобы максимизировать доход.
Таблица 1.3 Рассмотрим следующую задачу. Пусть на каждом шаге некоторой последовательности действий мы вправе выбрать один из двух вариантов возможных образов действий. При выборе первого варианта мы с вероятностью р1 получаем единицу прибыли, с вероятностью р2 — две единицы прибыли и с вероятностью р3 процесс заканчивается. При втором варианте эти вероятности соответственно равны р'1, р'2, p'3. Указать последовательность выборов, максимизирующую вероятность получения по крайней мере п единиц прибыли до завершения процесса. В некоторый начальный момент мы располагаем х долларами и сывороткой в количестве у, а также возможностью покупки добавочных количеств сыворотки в точно установленные моменты времени: t1 < t2 < .... За z долларов в каждый из моментов tk можно купить сыворотку в количестве ckz, где ск— монотонно возрастающая функция k. Задана вероятность вспышки эпидемии в период между моментами tk и tk.hl, причем в случае ее возникновения мы можем использовать только то количество сыворотки, которое уже имеется у нас на руках. Задача состоит в определении поведения закупки сыворотки, максимизирующего полную вероятность успешности борьбы с эпидемией. Требуется составить допустимый план работ на месяц с максимальным доходом. Вероятность успешного исхода э т ой борьбы при наличии сыворотки в количестве w считается известной. Условие ск > ск-х означает, что стоимость сыворотки уменьшается со временем вследствие совершенствования технологии производства. Построить математическую модель оптимального планирования объемов производства. Компания производит погрузчики и тележки. От одного погрузчика компания получает доход в размере $80 и от одной тележки в размере $40. Имеется три обрабатывающих центра, на которых выполняются операции металлообработки, сварки и сборки, необходимые для производства любого из продуктов. Для интервала планирования, равного месяцу, задана предельная производственная мощность каждого обрабатывающего центра в часах, a также количество часов, необходимое на этом центре для производства одного погрузчика и одной тележки. Эта информация задана в таблице 1.4. Таблица 1.4
Известно, что автомашина может взять с собой бензина в количестве, достаточном для прохождения расстояния в d миль. Чтобы она могла пройти расстояние в 2d миль по пустынной местности, ей необходимо создать на своем пути промежуточные заправочные пункты, завезя на них запасы бензина. Как следует их разместить, чтобы общие расходы бензина, необходимые для достижения пункта назначения, были минимальными, и чему равно общее расстояние, которое при этом придется пройти машине?
Газеты доставляются для продажи в ряд киосков. Предполагая, что функция распределения количества продаваемых в каждом из киосков газет известна и что определенное количество непроданных газет может быть возвращено с соответствующей уценкой, определить, сколько должно быть отпечатано экземпляров газеты и как они должны быть распределены по киоскам.
Человек стоит в очереди в ожидании обслуживания, причем перед ним стоят N человек. Ему известна полезность d от выстаивания очереди и вероятность р того, что за единицу времени будет обслужен один человек. С другой стороны, он терпит убыток величиной с, за каждую единицу времени, потраченную на ожидание. Задача состоит в определении такого поведения ожидания, которому соответствует максимальный средний доход.
. На трёх базах имеется запас сырья необходимого для производства четырех предприятий. На первой базе — 60 т., на второй — 90 т., на третьей — 140 т. Первому предприятию для производства требуется 40 т. сырья, второму — 30 т., третьему — 100 т., четвертому — 120 т. Найти оптимальный план задачи методом северо-западного угла, зная, что стоимость перевозок с первой базы на первое предприятие равна 4 ед., на второе — 2 ед., на третье — 3 ед., на четвертое — 4 ед., со второй базы на первое предприятие равна 2 ед., на второе — 4 ед., на третье — 3 ед., на четвертое — 5 ед., с третьей базы на первое предприятие равна 6 ед., на второе — 5 ед., на третье — 4 ед., на четвертое — 6 ед.
Нужно распределить между N предприятиями сумму a, выделенную для их инвестирования. Известно, что вложение средств в размере y в k -ое предприятие обеспечивает прибыль в размере dk(у). Целью распределения является получение максимального суммарного дохода. Решить задачу при N = 4, a = 300 при условии, что суммы инвестиций всегда кратны 50, а функции dk (у) для у = 50 • j (j = 0, 1, ..., 6) принимают значения, заданные в таблице 1.5. Таблица 1.5
На двух торговых базах А и В имеется 30 гарнитуров мебели, по 15 на каждой. Всю мебель требуется доставить в два мебельных магазина, С и D причем в С надо доставить 10 гарнитуров, а в D - 20. Известно, что доставка одного гарнитура с базы А в магазин С обходится в одну денежную единицу, в магазин D - в три денежных единицы. Соответственно с базы В в магазины С и D: две и пять денежных единиц. Составить план перевозок так, чтобы стоимость всех перевозок была наименьшей.
В пунктах А и В расположены кирпичные заводы, а в С и D - карьеры, снабжающие их песком. потребность заводов в песке меньше, чем производительность карьеров. Известно, сколько песка нужно каждому из заводов и сколько добывается в каждом карьере. Также известна стоимость перевозки 1 т песка из каждого карьера к заводам (числа на стрелочках). Нужно так спланировать снабжение заводов песком, чтобы затраты на перевозку были наименьшими.
Некоторому заводу требуется составить оптимальный план выпуска двух видов изделий, которые обрабатываются на четырех видах машин. Известны определенные возможности и производительность оборудования; цена изделий, обеспечивающая прибыль заводу, составляет 4 тыс. руб. за изделие I вида, 6 тыс. руб. - за изделие II вида. Составить план выпуска этих изделий так, чтобы от реализации их завод получил наибольшую прибыль.
Проблема проектирования эффективного перегонного устройства для производства тяжелой воды включает задачу о минимизации выражения VN=g(a1)+ g(a2)/a1+ g(a3)/a1a2+…+ g(am)/a1a2…am-1, Где аi подчинены следующим ограничениям: a) аi≥1 b) a1a2…am=x. Показать, что эта задача может быть сведена к функциональному уравнению fk+1(x)=min[g(a1) + fk(x/a1)/a1], a1≥1 и получить решение в случае g(y) = yb, b > 0.
Игрок имеет сумму денег х и хочет держать пари в N различных случаях. Существует вероятность рк того, что он может правильно предсказать исход в k-м случае. Ограничивается лишь ставка пари; это необходимо для того, чтобы игрок мог оплатить все свои проигрыши. Показать, что задачу максимизации ожидаемого им дохода можно свести к задаче максимизации линейной функции:
при условиях: a) xi ≥ 0 b) Пусть требуется определить план выпуска четырех видов продукции: A, B, C, D. Ресурсы трех видов: трудовые, материальные, финансовые, Количество каждого i-го вида ресурса для производства каждого j-го вида продукции, для изготовления которых используются ресдукции называют нормой расхода и обозначают aijj. Нормы расхода и наличие ресурсов приведены в таблице 1.6. Таблица 1.6.
Для выпуска единицы продукции, вида A требуется шесть единиц трудовых ресурсов, вида C- 11 единиц материальных ресурсов и т. д. Предприятие располагает 12000 единицами финансовых ресурсов, 2000 единицами материальных, 800 единицами трудовых. Исходя из рыночного спроса и производственно-технологических возможностей, заданы верхние и нижние предельные границы выпуска каждого вида продукции. На основании исходных данных требуется составить математическую модель для определения плана выпуска продукции.
Некоторому заводу требуется составить оптимальный план выпуска двух видов изделий, которые обрабатываются на четырех видах машин. Известны определенные возможности и производительность оборудования; цена изделий, обеспечивающая прибыль заводу, составляет 4 тыс. руб. за изделие I вида, 6 тыс. руб. - за изделие II вида. Составить план выпуска этих изделий так, чтобы от реализации их завод получил наибольшую прибыль. В таблице указано время, необходимое для обработки каждого из двух видов изделий на оборудовании всех четырех видов (таблица 1.7). Таблица 1.7
При выпуске продукции предприятие ограничено имеющимися ресурсами, количество которых обозначим m, а вектор ресурсов В = (b1, b2, ..., bт). Известны также технологические коэффициенты aij, которые показывают норму расхода i-го ресурса на производство единицы j-ой продукции. Эффективность выпуска единицы j-и продукции характеризуется прибылью pj. максимизирующий прибыль предприятия при заданных ресурсах. Частное предприятие планирует в течение N лет заниматься выпуском изделий, используя некоторое оборудование. В начале можно либо купить новое оборудование возраста Х0 = 0 лет и стоимостью р, либо подержанное оборудование возраста Х0 > 0 лет по его ликвидной стоимости р(Х0). Показатели эксплуатации оборудования включают: f (t) - стоимость произведенных за год изделий на оборудовании возраста t лет; r(t) - затраты на эксплуатацию в течение года оборудования возраста t лет. В процессе эксплуатации оборудование можно менять, продавая старое по ликвидной стоимости p(t) и покупая новое стоимостью р. В конце N -го года оборудование продается по ликвидной стоимости. Определить оптимальный возраст оборудования X0 при начальной покупке и оптимальный график его замены. Выполнить расчеты при N = 8, X0 = {0,1,2}, (p(t) = 6 при 0 < t < 6 ) f (t) = 30 — t/2, r(t) = 13 +t/2, p = 17, (p(t) = 2 при 7 < t < 10)
29 Предприятие, выпускает товары, изготавливая их отдельными партиями. Чем больше размер этих партий, тем относительно дешевле обходится выпуск. Поэтому в отдельные месяцы выгодно выпускать больше изделий, чем это нужно для удовлетворения спроса, а излишки хранить на складе для их реализации в последующие месяцы. За хранение в течение месяца каждой тысячи штук изделий нужно платить а = 1 усл.ед. Емкость склада ограничена величиной C = 4000 штук. Составить оптимальный план производства на N = 4 месяцев, при котором общая сумма затрат на производство и хранение была минимальной, а спрос на изделия - всегда удовлетворен. Объемы спроса по месяцам составляют mi (i = 1,..,N) изделий (при решении принять: 2000, 3000, 3000 и 2000). Начальные запасы готовых изделий составляют C0 = 2000. Размер производимых партий не может превышать p = 4000 изделий. Затраты, связанные с выпуском партий изделий объемом vt (i = 1,..,N) штук (принять: 1000, 2000, 3000 и 4000), определяются величинами zi (i = 1,.., N) (соответственно 13, 15, 17 и 19 усл.ед.).
Товар в количестве C = 100 ед. может реализовываться на трех рынках по ценам p1 , p2 и p3 за единицу продукции. Определить оптимальное распределение товара между рынками при следующих зависимостях цены от объема предлагаемой продукции xi на данном рынке: 40 -20 x1 при 0 < x1 < 20. 50 - 0.5 x2 при x2 > 30, p1(x1) = 0 при x1 > 20, p2(x2) = 30 при 0 < x2 < 30 p3(x3) = 30 - 0.3x3
Используя уравнения Беллмана, составить расчетную схему решения задачи максимизации суммарной прибыли от работы k цехов, выпускающих изделия разных видов. Прибыль от выпуска x изделий j -го вида (он производятся j -м цехом) определяется значением Pj (x) (таблица 1.8). Изготовление одного изделия j -го вида требует определенного количества сырья m типов, а именно Cj1, ... , Cjm. Запасы этого сырья, общие для всех цехов, составляют z1, ... , zm . Решить задачу при следующих данных: K = 3, m = 2, расходы сырья для изделия первого типа: C11 = 2, C12 = 4 ; второго: C21 = 4, C22 = 2; третьего: C31 = 1, C32 = 3; а запасы составляют z1 = 10, z2 = 12. Таблица 1.8 Значения прибыли P ( x)
Имеется некоторое производство, которое ежедневно обеспечивается поставками сырья в количествах Р1, Р2, … , Pn • Излишки сырья хранятся на складе емкостью E. Начальное количество сырья на складе задано и составляет E0. Обозначим X1, X2, …, Xn — объемы сырья, ежедневно забираемые на производство. Общее количество перерабатываемого за N дней сырья известно и равно A. По известному графику поставок сырья Р1, Р2, …, Pn составить график его потребления X1, X2, … , Xn , минимизирующий неритмичность производства, понимаемую как Ө=∑(xi – A/N)2 . Сырье следует считать штучным. Решить задачу при N = 5, E0 = 2, E0 = 5 E0 = 10, Р1 = 1, Р2 = 1, Р3 = 1, Р4 = 6, Р5 = 7.
Предприятие функционирует N лет. Начальный капитал равен a . Каждый год некоторая часть и* имеющейся суммы пускается в оборот с условием возврата в кассу в конце года суммы в размере рj (и*). Кроме того, из дохода выплачивается сумма fj (и*) в качестве вознаграждения работникам. Найти оптимальные значения U1, U2, ..., Un , максимизирующие сумму выплаченных вознаграждений. Выполнить расчет при N = 3, f1(u) = 0.1 • и 2, р1(u) = 0.7• и, f2(u) = 0.2• и, р2(и) = 0.3 • и, f3(u) = и, р3(u) = 0. Газы из сопла ракеты вылетают с постоянной скоростью C. Сопло подвешено на оси, и направление выброса газов можно регулировать. В предположениях, что движение ракеты является плоским, происходит в безвоздушном пространстве и вектор ускорения свободного падения g является постоянным, найти оптимальное управление тягой ракеты (a(t); и(t)), 0 < и(t) < A, максимизирующее: а) дальность полета ракеты; б) высоту подъема ракеты. Здесь a(t) - угол между горизонтом и прямой, вдоль которой происходит выброс газов в момент времени t .
Телевизионная компания намерена арендовать телевизионные линии связи для объединения части своих станций в единую сеть. Телевизионные линии связи существуют между любыми двумя станциями, и известна стоимость их аренды, которая, вообще говоря, различна для различных пар станций.. Показать, что для создания сети с минимальными затратами следует среди еще не включенных в сеть линий связи выбирать ту, арендная плата за которую минимальна и которая не замыкает кольца уже работающих линий.
Догоняющий находится в i -той клетке из 5 клеток, образующих круг. За один такт он с вероятностью р = 1/2 перемещается по часовой стрелке в соседнюю клетку, с вероятностью q = 1/3 перемещается против часовой стрелки в соседнюю клетку, с вероятностью r = 1/6 остается на месте. Убегающий находится в j -той клетке и на каждом такте может выбрать одну из трех стратегий поведения: (a) переместиться по часовой стрелке в соседнюю клетку; (b) остаться на месте; (с) переместиться против часовой стрелки в соседнюю клетку. Расстояние между догоняющим и убегающим определяется по формуле d = i — j . Определить стратегию убегающего на три такта вперед, максимизирующую сумму расстояний между догоняющим и убегающим.
Состояние продуктивности земли, используемой фермером, может быть (a) хорошим,(b) удовлетворительным, (с) плохим. Вероятности перехода продуктивности земли из одного состояния в другое без проведения агротехнических мероприятий за один сезон заданы матрицей P1. Однако фермер может провести комплекс агротехнических мероприятий, и тогда вероятности перехода продуктивности земли из одного состояния в другое за один сезон будут заданы матрицей P2. Матрицы доходов для двух стратегий поведения: D1, D2 – таблице 1.9. Найти оптимальную стратегию фермера на 4 сезона. Таблица 1.9
Студент уже сдал один экзамен на 4, но ему предстоит сдать еще три экзамена. При подготовке к экзаменам он из-за недостатка времени может выбрать одну из следующих двух стратегий: либо выучить часть материала довольно хорошо, либо пройтись быстро по всему материалу. Определить оптимальную в смысле набранных баллов стратегию поведения студента на оставшиеся три экзамена, если матрицы вероятностей получения оценок 5, 4, 3, 2 в зависимости от предыдущей оценки для двух стратегий имеют вид (таблица 1.10). Таблица 1.10
Электростанция имеет L агрегатов. Предположим, что производительность одного агрегата за неделю равна C , а единица произведенной электроэнергии продается по цене b. График оплачиваемого производства электроэнергии по неделям задан: Р1, Р2,..., Pn, и нарушаться не должен. Избыточно произведенная электроэнергия не оплачивается. Затраты на поддержание в рабочем состоянии 1 агрегатов в течение недели равны r(1), затраты на консервацию D1 агрегатов составляют Pk(D1). Затраты на пуск равны Pп(D1). Составить рекуррентные уравнения Беллмана для определения оптимального графика эксплуатации агрегатов. Составить рекуррентные уравнения Беллмана для предыдущей задачи при следующем изменении ее условий. Вначале в фонд развития вносится сумма денег A. Средства на покупку сырья берутся из фонда развития. Кирпич производится не для личного использования, а для продажи по цене B за штуку ( в ценах стартовой недели). При этом 50% получаемой от продажи суммы добавляется к оставшимся в фонде средствам, а остальные 50% используются на оплату рабочим, налоги и потребление. Необходимо составить рекуррентные уравнения Беллмана, позволяющие решить задачу об оптимальном выделении средств на закупку сырья для максимизации суммы денег в фонде развития к концу N -й недели. Господин M, желая построить коттедж, одолжил у своего друга на N недель мини-установку по производству дешевого кирпича с функцией производительности f (X) штук в неделю, где X - количество использованного сырья. Следует считать, что производная функции f(X) положительна и убывает при увеличении x. Перед началом производства имелась сумма денег A . Стоимость единицы сырья в ценах стартовой недели равна C . Коэффициент инфляции за неделю равен а > 1. Сырье покупается еженедельно в количествах X1, X2, ..., Xn . По окончании N -й недели на оставшиеся неистраченные деньги покупается готовый более дорогой кирпич по цене B за штуку (в ценах стартовой недели). Необходимо составить рекуррентные уравнения Беллмана для определения оптимальных размеров закупки сырья, приводящих к максимизации общего количества полученного кирпича. Ракета с массой m движется по прямой вне поля силы тяжести. Реактивный двигатель работает в импульсном режиме. Сообщаемая величина импульса U е [—V, V], а затраты топлива пренебрежимо малы по сравнению с массой корабля. Считать, что порция топлива сгорает мгновенно. Найти значения U1, U2, ... , Un , при которых ракета из состояния покоя перейдет в другое состояние покоя, максимально удаленное от начального. Принять, что приращение скорости, полученное в k -й момент времени, начинает оказывать влияние на приращение координаты только в следующий (k +1) -й момент времени. Решить задачу при N = 3 и N = 5; m = 1, V = 10. Интервал между импульсами принять равным единице. Указание: сообщение системе импульса U изменяет ее количество движения (произведение массы на скорость) на величину U .
Ракета-носитель с N ступенями имеет общую массу M , включающую массу m выводимого на орбиту космического аппарата и топливо. Вес оболочек ступеней считается равным нулю. Обозначим вес топлива в ступенях ракеты через U1, U2, ..., Un . Будем считать, что прирост скорости ракеты при сгорании k-ой ступени пропорционален отношению Ukj(m + Un + ... + Uk). Требуется определить оптимальное распределение топлива по ступеням ракеты. Выполнить расчеты при N = 3, M = 64, m = 1.
Составить оптимальный план ежегодного распределения средств между двумя предприятиями в течение N лет, если начальная сумма средств равна A, доходы от вложения средств x1 и x2 в предприятия составляют f1(x1) и f2 (x2 ) . Вложенные средства возвращаются в общую кассу для перераспределения в размере 60% от x1 для первого и 20% от x2 для второго предприятия. Каждый год все имеющиеся в общей кассе средства полностью перераспределяются с точностью до остатка, меньшего А; x1 и x2 выбираются кратными А. Решить задачу при N = 3, A = 400, А = 50 и значениях функций f1( x) и f2 (x2) из таблицы 1.11. Таблица 1.11 Значения функций f1(x1) и f2(x2)
Технологическая цепочка изготовления изделия включает N операций, выполняемых на автоматизированных участках конвейерной обработки. Устройство, выполняющее операции на i -ом участке, имеет вероятность работы без отказа р^ и стоимость cj. Для повышения надежности на участке можно установить mi дублеров, повысив надежность участка до значения Pi (mi) = 1 — (1 — Pi )1+mi . Средства, выделенные на установку устройств-дублеров, ограничены значением C. Решить задачу о выборе оптимального количества дублеров, приводящем к максимизации надежности всей технологической цепочки. При решении принять N = 3, C = 17, P1 = 0.5, P2 = 0.3, С1 = 6, С2 = 4, С3 = 4. Для упрощения расчетов принять приближенные значения функций Pi (m) из таблицы 1.12. Таблица 1.12 Значения функции Pi (m)
Решено одновременно заменить все осветительные электрические лампочки в рабочем помещении. Обозначим через а издержки от замены электролампочек, а через g(x)— потери, которые вызваны недостаточностью освещения, когда между двумя заменами проходит время х. Пусть принято решение заменять лампочки в течение интервала Т в следующие моменты времени: х1, х1 + х2, ..., x1 + x2 + … +xn = Т, где число п определено заранее. Эффективность такой программы действий измеряется средней суммой потерь
Каким должно быть оптимальное поведение?
Следователь, устанавливающий личность убийцы, имеет N свидетелей различной степени надежности, причем один из них является убийцей. Обозначим через pi вероятность того, что i-й свидетель ответит правду в любой момент на любой обращенный к нему вопрос. Следователь допрашивает свидетелей в некотором порядке. При этом первому из допрашиваемых он задает некоторый вопрос, а каждому следующему задает либо прямой вопрос, либо вопрос относительно истинности показаний предыдущих свидетелей. Предполагая, что следователю разрешается при каждом допросе задавать один вопрос и что i-му свидетелю для ответа на вопрос требуется время указать, в каком порядке свидетели должны допрашиваться и какие вопросы им следует задать, чтобы максимизировать вероятность обнаружения убийцы в течение заданного промежутка времени Т. На каждом шаге некоторой последовательности действий мы вправе выбрать один из двух вариантов возможных образов действий. При выборе первого варианта мы с вероятностью р1 получаем единицу прибыли, с вероятностью р2 — две единицы прибыли и с вероятностью р3 процесс заканчивается. При втором варианте эти вероятности соответственно равны р'1, р'2, р'3,. Указать последовательность выборов, максимизирующую вероятность получения по крайней мере п единиц прибыли до завершения процесса.
Имеется n, вообще говоря, не одинаковых изделий, которые должны быть обработаны на ряде установок различных типов (числом т). Порядок, в котором эти установки должны использоваться, имеет существенное значение, так как некоторые процессы обработки должны быть выполнены раньше других. При заданном времени аij (i= 1, 2, ...» п; j=1,2, т), необходимом для обработки i-го изделия на j-й установке, требуется определить порядок, в котором эти изделия должны запускаться в обработку, чтобы общее время, необходимое для выпуска готовой продукции, было минимальным.
Для исправления ошибки, обнаруженной на i-й стадии производственного процесса, требуется время ti, а связанные с этим исправлением расходы равны сi. Определить сумму, которую целесообразно выделить на приобретение контрольной аппаратуры, а также распределение последней между операциями, если известны величина заработной платы и стоимость работы оборудования, приходящиеся на одно изделие, а также убытки от выработки дефектного изделия (скажем, z).
Владелец ресторана располагает двумя различными способами стирки салфеток; при быстром способе стирка занимает q дней и обходится в с центов за штуку; медленный же способ стирки требует р > q дней и обходится в d <с центов за штуку. Предполагая, что владелец ресторана заранее знает число посетителей, которых он должен будет обслужить в любой из дней N -дневного периода, и что он должен обеспечить салфеткой каждого посетителя. Определить, сколько салфеток он должен купить и как должен отдавать их в стирку, чтобы минимизировать общие расходы в течение N-дневного периода. Рассмотреть сначала случаи, когда p = q + 1 и p = q + 2.
Имеется ряд „источников” или “пунктов отправления”, S1 S2, …, Sm и ряд «стоков“, или „пунктов назначения", T1 Т2, ..., TN. В каждом источнике Si имеется некоторое количество материала xi, которое должно быть перевезено в различные пункты назначения, причем так, чтобы общее количество материала, доставляемое в пункт Tj, равнялось заданному требованию yj на него в этом пункте. Предполагается, что
Поиск по сайту: |

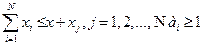

 . При данных расстояниях dij между пунктами отправления и пунктами назначения и в предположении, что стоимость перевозки единицы количества материала между пунктами Si и Tj равна dij определить план перевозок, минимизирующий общую стоимость удовлетворения требований. Показать, что рассмотренная выше задача эквивалентна минимизации линейной формы
. При данных расстояниях dij между пунктами отправления и пунктами назначения и в предположении, что стоимость перевозки единицы количества материала между пунктами Si и Tj равна dij определить план перевозок, минимизирующий общую стоимость удовлетворения требований. Показать, что рассмотренная выше задача эквивалентна минимизации линейной формы  при ограничениях:
при ограничениях:

