Раздел 6. Оптимизации задач методом ветвей и границ

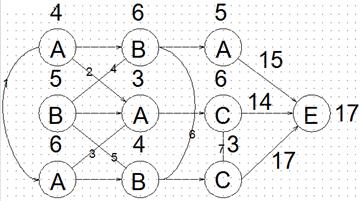
Метод ветвей и границ – метод оптимизации переменных целевой функций универсального типа – от аналитического до графоаналитического и алгоритмического. Ниже приведено решение оптимизационной задачи минимизации времени окончания трёх процессов на трёх станках методом ветвей и границ . На рис. 6.1 приведен процесс одновременной обработки деталей α, β и γ на трёх станках A,B и C. Порядок прохождения станков для каждой детали – разный и указан на графе дугами (линиями со стрелками). Условие невозможности одновременной обработки разных деталей на одном и том же станке указано на графе рёбрами (линиями без стрелок). Операция обработки детали на станке указана кружком, а длительность обработки указана числом в условных единицах (у.е.) над каждым кружком. Конец выполнения всех трёх процессов указан кружком с буквой E. Числами над последними дугами указана длительность каждого процесса. Числом справа от E указана максимальная длительность из трёх процессов при условии, что станков каждого типа столько, что все процессы могут выполняться одновременно во времени. Это число, равное 15, является нижней границей минимального времени выполнения всех процессов. Само минимальное время будет больше или равно 15 из-за наличия времени ожидания обработки деталей на станках в реальном случае, когда используется только по одному станку каждого типа. Нижняя граница меняется при изменении очерёдности обработки конфликтующих деталей на станке одного типа. Это позволяет найти оптимальную очерёдность обработки всех деталей на станках всех типов, выбирая на каждом этапе решения задачи ту очерёдность, которая соответствует минимальному значению нижней границы времени выполнения всех процессов. С каждым последующим этапом выбираемое значение нижней границы, во-первых, не уменьшается, а во-вторых. приближается к минимальному значению времени окончания всех процессов. На последнем этапе нижняя граница становится равной минимальному времени выполнения всех процессов, а соответствующая ей очерёдность обработки всех деталей на всех станках – оптимальной.

Рассмотрим пример решения такой задачи, изображённой на рис. 6.1, методом ветвей и границ.

Рис. 6.1 Исходная постановка задачи (Mvg_15)

На рис. 6.2 все рёбра пронумерованы и должны быть постепенно заменены дугами, направленными вверх или вниз так, чтобы получить минимальное время выполнения всех процессов. На первом этапе заменяется дугой вниз или вверх ребро с номером 1.

При замене этого ребра дугою вниз нижний процесс ждёт момента окончания обработки детали α на станке A. Вместе с ожиданием время выполнения нижнего процесса увеличится на 4 у.е. и станет равным 17 у.е. Для этого случая нижняя граница станет равной 17 у.е.

Рис. 6.2 Замена первого ребра дугою вниз (Mvg1d_17)

Если первое ребро заменить дугою вверх (см. рис. 6.3), то ожидать момента окончания обработки детали γ на станке A будет верхний процесс, в результате чего длительность его увеличится на 6 у.е. и станет равной 21у.е. Эта величина и станет нижней границей времени окончания всех процессов. При выборе этого варианта минимальное время ни в коем случае не будет меньше 21у.е., в то время как в предыдущем варианте результат может оказаться меньше 21у.е. Поэтому при выполнении следующих этапов первое ребро заменяется дугою вниз

Рис. 6.3 Замена первого ребра дугою вверх (Mvg1v_21)

На следующем этапе заменяется дугою вниз или вверх второе ребро при условии, что первое ребро заменено дугою вниз. На рис.6.4 второе ребро заменено дугою вниз. Длительность процесса обработки детали β не увеличится, так как станок A

Рис. 6.4 Замена второго ребра дугою вниз (Mvg1d2d_17)

освободится на 1 у.е. раньше, чем закончится обработка детали β на станке B. Поэтому значение нижней границы в этом случае останется равным 17.

При замене второго ребра дугою вверх (см. рис. 6.5) обработка детали α на станке A может начаться через (5+3) у.е., а обработка детали γ на станке A может начаться через (5+3+4) у.е. Поэтому верхний процесс закончится через 23 у.е., а нижний процесс – через 29 у.е. Нижняя граница в этом случае будет равна 29 у.е.

Рис. 6.5 Замена второго ребра дугою вверх (Mvg1d2v_29)

На третьем этапе заменяем третье ребро дугою вниз или вверх при условии, что первое и второе ребра заменены дугою вниз. На рис. 6.6 третье ребро заменено дугою вниз, а на рис. 6.7 – дугою вверх. В первом случае обработка детали γ на станке A

Рис. 6.6 Замена третьего ребра дугою вниз (Mvg1d2d3d_21)

Рис. 6.7 Замена третьего ребра дугою вверх (Mvg1d2d3v_19)

Ждёт (5+3) у.е. и минимальная граница равна 25 у.е. Во втором случае обработка детали β на станке A ждёт (4+6) у.е. и процесс обработки β заканчивается через 19 у.е., обеспечивая минимальную границу выполнения всех процессов в этом случае равной 19 у.е.

На четвёртом этапе заменам дугами вниз или вверх подвергается четвёртое ребро.

На рис. 6.8 третье ребро заменено дугою вниз, а на рис. 6.9 – дугою вверх. В первом

случае обработка детали β на станке A будет ждать (4+6) у.е. и весь процесс закончится через 24 у.е. с минимальной границей, тоже равной 24 у.е. Во втором случае

Рис. 6.8 Замена четвёртого ребра дугою вниз (Mvg1d2d3v4d_24)

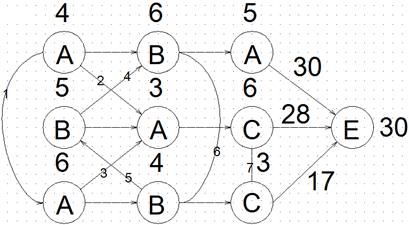
Рис. 6.9 Замена четвёртого ребра дугою вверх (Mvg1d2d3v4v_19)

обработка детали α на станке B будет ждать 5 у.е. и верхний процесс закончится через 16 у.е., а обработка детали β на станке A будет ждать (4+6) у.е., а весь процесс закончится через 19 у.е., обеспечивая минимальную границу, равную 19 у.е.

Поэтому на пятом этапе замена пятого ребра дугами вниз или вверх выполняется при условии, что четвёртое ребро заменяется дугою вверх, а замена первых трёх рёбер дугами остаётся прежней. На рис. 6.10 пятое ребро заменено дугою вниз, а на рис.

Рис. 6.10 Замена пятого ребра дугою вниз (Mvg1d2d3v4v5d_19)

6.11 – дугою вверх. Замена пятого ребра дугою вниз не увеличивает длительность нижнего процесса и нижняя граница остаётся равной 19 у.е. Замена этого ребра дугою вверх вызывает ожидание начала среднего процесса на (4+6+4) у.е. и ожидание начала обработки детали α на станке B на (4+6+4+5) у.е., что приводит к окончанию обоих процессов соответственно через 28 и 30 у.е. с нижней границей, равной 30 у.е.

Поэтому на шестом этапе замена шестого ребра дугами вниз или вверх выполняется

Рис. 6.11 Замена пятого ребра дугою вверх (Mvg1d2d3v4v5v_30)

при замене пятого ребра дугою вниз с прежними заменами дугами первых четырёх рёбер (см. рис. 6.12, 6.13). Замена шестого ребра дугою вниз вызывает ожидание начала обработки детали γ на станке B на (5+6) у.е., что вызывает увеличение длительности нижнего процесса до 18 у.е. При этом нижняя граница остается равной 19 у.е.

Рис. 6.12 Замена шестого ребра дугою вниз (Mvg1d2d3v4v5d6d_19)

Рис. 6.13 Замена шестого ребра дугою вверх (Mvg1d2d3v4v5d6v_25)

Замена шестого ребра дугою вверх вызывает ожидание обработки детали α на станке B на (4+6+4) у.е., что приводит к увеличению длительности верхнего процесса и нижней границы до 25 у.е.

Поэтому на седьмом этапе замена седьмого ребра на дугу вниз или вверх выполняется для замены шестого ребра дугою вниз при прежних заменах дугами первых пяти ребер (см. рис. 6.14, 6.15). Замена седьмого ребра на дугу вниз не увеличивает длительность нижнего процесса. Поэтому нижняя граница осталась равной 19 у.е.

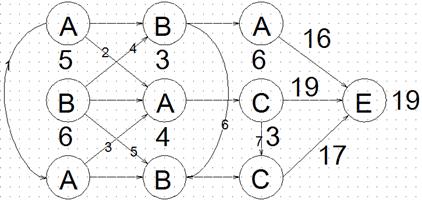
Рис. 6.14 Замена седьмого ребра дугою вниз (Mvg1d2d3v4v5d6d7d_19)

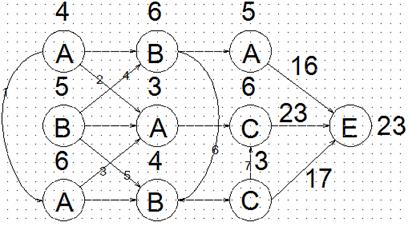
Рис. 6.15 Замена седьмого ребра дугою вверх (Mvg1d2d3v4v5d6d7v_23)

Замена седьмого ребра дугою вверх вызывает ожидание начала обработки детали β на станке C, равное (4+6+4+3) у.е., что приводит к увеличению среднего процесса и нижней границы до 23 у.е. Поскольку заменены дугами все ребра, то нижняя граница в обоих случаях совпадает с временем окончания всех процессов. Из двух времён выбираем меньшее 19 у.е. Это – наименьшее время обработки всех процессов, а соответствующие ему дуги представляют оптимальную очерёдность обработки деталей α, β и γ на всех трёх станках.

Варианты заданий по оптимизации очерёдности операций

Поиск по сайту: