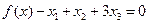|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Раздел 4. Оптимизация задач линейного программирования
Задача условной оптимизации называется задачей линейного программирования (ЛП), если все функции – целевая и ограничений - являются линейными:
при ограничениях
где заменяя равенство двумя неравенствами , можно придти к стандартной форме. Кроме того, взяв вместо f(x) функцию –f(x), можно получить задачу на минимум. Приведем основные свойства задачи ЛП. Допустимое множество решений задачи ЛП либо пусто, либо является выпуклым многогранником в Rn (как пересечение полупространств, описываемых ограничениями-неравенствами). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник. Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации - ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение. Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечно много точек максимума или минимума). Универсальный метод решения задач ЛП называется симплекс-методом. Применение этого метода и его наиболее часто встречающейся модификации - двухфазного симплекс-метода мы поясним на примерах. Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности ограничений задачи
Рис. 4.1 Задача линейного программирования ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум). Для ускорения решения необходимо при переходе от одной вершины к другой двигаться по такому ребру многогранника, при перемещении по которому изменение значения целевой функции максимально.
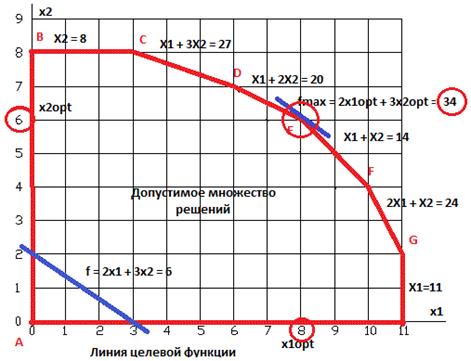
Пример решения 4.1 Решить следующую задачу ЛП в канонической форме симплекс-методом, изображенную на рис. 4.1. Составим систему линейных неравенств, образующих допустимое множество решений. Заменим обозначение целевой функции f(x) на обозначение переменной X0, приравняем её значение нулю и перенесём её переменные 2X1 и 3X2 влево от знака равно со знаком минус. X0 - 2X1 - 3X2 = 0 . Выпишем ограничительные неравенства в виде системы. X0 - 2X1 - 3X2 = 0 X2 ≤ 8 X1 + 3 X2 ≤ 27 X1 + 2 X2 ≤ 20 X1 + X2 ≤ 14 2 X1 + X2 ≤ 24 X1 ≤ 11
. Рис. 4.2 Значение целевой функции в оптимальной точке (8, 6)
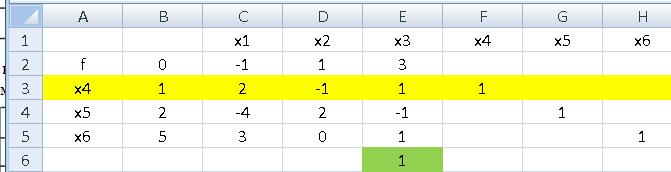
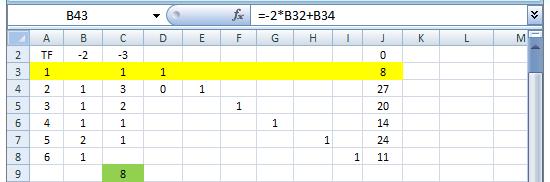
В каждое неравенство введём по одной положительной переменной X3, …, X8,дополняющей значение левой части каждого неравенств до равенства правой части. X0 - 2 X1 - 3X2 = 0 X2 + X3 = 8 X1 + 3X2 + X4 = 27 X1 + 2X2 + X5 = 20 X1 + X2 + X6 = 14 2 X1 + X2 + X7 = 24 X1 + X8 = 11 Для однозначного решения системы из шести уравнений с восемью переменными присвоим двум переменным X1 и X2 значение, равное нулю. Остальные (базисные) переменные станут равными значениям правых частей уравнений. Решение системы соответствует вершине А выпуклого многоугольника (симплекса) допустимых решений системы, совпадающей с началом координат (см. рис. 4.2). Такой вид системы, в которой целевая функция выражена через переменные с нулевыми значениями (X1 и X2), а в остальных ограничительных уравнениях по одной ненулевой переменной (X3, …, X8), называется базисным. Он позволяет определить значение целевой функции в вершине симплекса A и ребро многоугольника, при движении по которому значение целевой функции увеличивается максимально. Это ребро совпадает с X2. Переместимся по нему до следующей вершины B. Значение X2 определяем, как минимальное отношение правой части в каждом уравнении к коэффициенту при переменной X2. X2 = min (8/1, 27/3, 20/2 , 14/1, 24/1, 11/0) = 8 Уравнение, которому соответствует минимальное отношение, называется опорным и выделяется цветом. Умножая его на соответствующее число и складывая с целевой функцией или с каждым из остальных уравнений, добиваемся того, чтобы в них коэффициент при X2 был равен нулю. Тогда система снова примет базисный вид для следующей вершины симплекса B и по знакам коэффициентов в целевой функции можно будет определить, оптимальная ли эта вершина, или нет. Для оптимальной вершины все коэффициенты в целевой функции будут положительными и задача будет решена. Если коэффициенты отрицательны, то выбирается отрицательный коэффициент, наибольший по абсолютной величине. Ему соответствует ребро симплекса, при перемещении по которому значение целевой функции увеличивается максимально. В нашем случае это переменная Х1 (ребро ВС).По аналогии с X2 определяется минимальное значение X1, при котором текущая точка перемещается в следующую вершину С. Выделяется соответствующее ей опорное уравнение и с помощью него обнуляются коэффициенты при X1в целевой функции и в остальных ограничительных уравнениях. Получив тем самым базисный вид системы для этой вершины симплекса, определяем по виду целевой функции, оптимальна ли эта вершина. И если нет, повторяем выбор переменной с отрицательным коэффициентом, исключая её из числа нулевых (небазисных) в системе до тех пор, пока в уравнении целевой функции все переменные не будут с положительными коэффициентами. Первое преобразование системы в базисную форму для вершины B. X0 - 2X1 + 3X3 = 24 X2 + X3 = 8 X1 - 3 X3 + X4 = 3 X1 - 2 X3 + X5 = 4 X1 - X3 + X6 = 7 2X1 - X3 + X7 = 16 X1 + X8 = 11 X1 = min (8/0, 3/1, 4/1 , 7/1, 16/2, 11/1) = 3 Второе преобразование системы в базисную форму для вершины C. X0 - 3X3 + 2X4 = 30 X2 +X3 = 8 X1 -3X3 +X4 = 3 X3 -X4 + X5 = 1 2 X3 -X4 + X6 = 4 5 X3 -2X4 + X7 = 10 3 X3 - X4 + X8 = 8 X3 = min (8/1, 3/-3, 1/1 , 4/2, 10/5, 8/3) = 1 Третье преобразование системы в базисную форму для вершины D. X0 -X4 + 3X5 = 33 X2 + X4 - X5 = 7 X1 -2X4 +3X5 = 6 X3 - X4 +X5 = 1 2 X4 -2X5 +X6 = 2 3 X4 -5X5 +X7 = 5 2 X4 - 3X5 +X8 = 5 X4 = min (7/1, 6/-2, 1/-1 , 2/2, 5/3, 5/2) = 1 Четвёртое преобразование системы в базисную форму для вершины E. X0 2X5 + 1/2X6 = 34 X2 - X6 = 6 X1 + 2X5 + 3X6 = 8 Это последнее преобразование системы в базисную форму, потому что в уравнении целевой функции коэффициенты при нулевых переменных X5 и X6 – положительны. Максимальное значение целевой функции равно 34, а оптимальные значения перменных X1 и X2 равны соответственно 8 и 6. Этим значениям, полученным аналитически, соответствуют значения X0, X1 и X2, полученные графически (см.рис.4.2) Преобразования системы уравнений в базисную форму удобно выполнять в приложении Excel. На рис.4.3 показана исходная система уравнений. Нулевую переменную X2 изменяем до 8.
Рис. 4.3 Значение целевой функции в точке (0, 0)
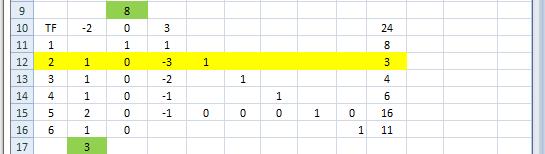
На рис. 4.4 показано первое преобразование системы в канонический вид для следующей вершины. Нулевую переменную X1 увеличиваем до 3.
Рис. 4.4 Значение целевой функции в точке (0, 8)
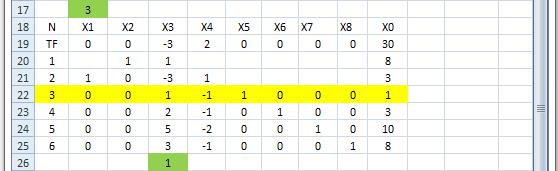
На рис. 4.5 показано второе преобразование системы в канонический вид для следующей вершины. Нулевую переменную X3 увеличиваем до 1.
Рис.4.5 Значение целевой функции в точке (3, 8) На рис 4.6 показано третье преобразование системы в канонический вид для следующей вершины. Нулевую переменную X4 увеличиваем до 1.
Рис. 4.6 Значение целевой функции в точке (6, 7) На рис. 4.7 показано последнее преобразование системы в канонический вид для следующей вершины. Коэффициенты при нулевых переменных X5 и X6 - положительны. Значит целевая функция – максимальна, а переменные X1 и X2 – оптимальны и равны соответственно 8 и 6.
Рис. 4.7 Значение целевой функции в оптимальной точке (8, 6) Варианты заданий для этого примера приведены в приложении 4.1
Пример 4.2 Решить задачу ЛП в канонической форме симплекс-методом.
Задача ЛП имеет каноническую форму, если все ограничения (кроме условий неотрицательности переменных) имеют вид строгих равенств, а все свободные члены неотрицательны. Чтобы найти начальное допустимое базисное решение, систему (2.4.6) нужно привести к "диагональному" виду. В данном примере легче всего назначить нулевые значения переменным x1 и x3, а значения остальных выразить через них. x2 + x1 + x3 = 40 x4 + x1 = 20 (4.3) x5 - x.1 - x3 = 10 x6. + x3 = 30
Подставив их в уравнение целевой функции выразим её через x1 и x3. f(x) +7x1 +14x3 =880 Теперь при помощи составляем начальную симплекс-таблицу (таблица 4.1): Таблица 4.1
В нулевую строчку записаны коэффициенты соответствующих переменных при целевой функции. Так как все переменные неотрицательны, то целевая функция тем меньше, чем меньше эти коэффициенты. Отсюда критерий оптимальности: допустимое базисное решение (д.б.р.) (x0) оптимально, если в нулевой строчке нет ни одного строго положительного числа (не считая значения целевой функции (880)). Так как x0 неоптимальное, то надо перейти к другой вершине многогранника допустимых решений (построить новое д.б.р.). Для этого нужно найти ведущий элемент и провести симплексное преобразование (таково требование симплекс-метода). Ведущий элемент таблицы стоит в пересечении ведущего столбика (столбец с наибольшей положительной оценкой) и ведущей строки (строки, соответствующей минимальному соотношению элементов нулевого столбика к соответствующим элементам (строго положительным) ведущего столбика). В таблице 1 ведущий столбик - третий столбик, и ведущая строка - четвертая строка (min{40/1,30/1}=30/1) обозначены стрелками, а ведущий элемент - кружочком. Ведущий элемент показывает, что базисную переменную x6 нужно заменить на небазисную x3 . Тогда новыми базисными переменными будут x2, x3, x4, x5, , а небазисными -x1, x6, . Это и означает переход к новой вершине многогранника допустимых решений. Чтобы найти значения координат д.б.р. x00 нужно строить новую симплекс-таблицу и провести в ней элементарные преобразования: а) все элементы ведущей строки поделить на ведущий элемент, превратив этим самым ведущий элемент в 1 (для простоты выкладок); В результате в нулевом столбце получены значения новых базисных переменных x2, x3, x4, x5, (см. таблицу 4.2 ) - базисные компоненты новой вершины x00 (небазисные компоненты x1=0, x6=0, ). Таблица 4.2
Как показывает таблица 2, новое базисное решение x00=(0,10,30,20,40,0) неоптимально (в нулевой строке есть неотрицательная оценка 7). Поэтому с ведущим элементом 1 (см. таблицу 2 ) строим новую симплекс-таблицу, т.е. строим новое д.б.р. Таблица 4.3
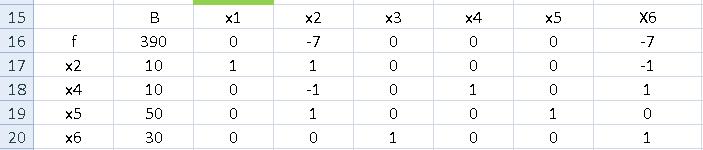
Таблице 3 соответствует д.б.р. x000=(10,0,30,10,50,0) и оно оптимально, т.к. в нулевой строчке нет положительных оценок. Поэтому f(x000)=390 есть минимальное значение целевой функции. Ответ: x000=(10, 0, 30, 10, 50, 0) - точка минимума, f(x000)=390 . Симплексные преобразования новых базисных решений удобно выполнять в приложении Excel. На рис.4.8 показана таблица коэффициентов для исходной системы в базисном виде для вершины (x1 = 0, x3 =0). )Коэффициенты при нулевых переменных x1 и x3 -положительны. Значит целевая функция – не минимальна. Выбираем перемещение по ребру x3 до следующей вершины симплекса, в которой Х3 = 30.
Рис. 4.8 Значение целевой функции в вершине (x1 = 0, x3 =0). На рис. 4.9 показана таблица коэффициентов для следующей системы в базисном виде для вершины (x1 = 0, x6 =0).
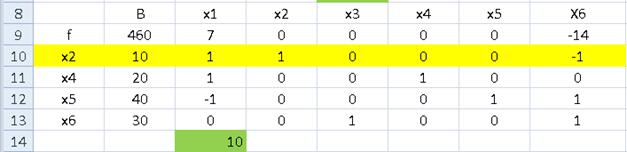
Рис. 4.9 Значение целевой функции в вершине (x1 = 0, x6 =0). На рис. 4.10 показана таблица коэффициентов для последней системы в базисном виде для вершины (x2 = 0, x6=0).
Рис. 4.10 Значение целевой функции в вершине (x2 = 0, x6 =0). Отрицательность коэффициентов при нулевых переменных (x2 = 0, x6=0) в целевой функции f(x) свидетельствует о достижении её минимального значения в этой вершине симплекса. Варианты заданий для этого примера приведены в приложении 4.2
Пример 4.3. Решить следующую задачу ЛП в неканонической форме симплекс-методом: f(x) = x1 - x2 - 3x3 → min при ограничениях 2x1 – x2 + x3 ≤ 1 -4x1 + 2x2 – x3 ≤ 2 3x1 +x3 ≤ 5 Умножая обе части на -1 и прибавляя в левые части системы дополнительные (или слабые) переменные f(x) = x1 - x2 - 3x3 → min при ограничениях 2x1 – x2 + x3 + x4 = 1 -4x1 + 2x2 – x3 + x5 = 2 3x1 +x3 x6 = 5 x1,…, x6 ≥ 0 Так как все слабые переменные входят со знаком "+", то их можно взять в качестве базисных и составить н.д.б.р. x0=(0,0,0,1,2,5) . В данном случае исключать базисные переменные из целевой функции нет надобности (так как они в ней отсутствуют), поэтому целевую функцию записываем сразу в виде
(требование симплекс-метода). С помощью н.д.б.р. x0 и ограничений составим начальную симплекс-таблицу 4.4 (здесь f(x0)=0 ). Таблица 4.4
Так как x0 неоптимален (в нулевой строке есть положительные числа 1 и 3), то с обозначенным ведущим элементом строим новое д.б.р. И так далее. На четвертой итерации (шаге) получаем таблицу 4.5: Таблица 4.5
На рис. 4.11 показана таблица коэффициентов для исходной системы в базисном виде для вершины (x1 = 0, x2 = 0, x3 = 0). )Коэффициенты при нулевых переменных x2 и x3 - положительны. Значит целевая функция – не минимальна. Выбираем перемещение по ребру x3 до следующей вкршины симплекса, в которой x3 = 1.
Рис. 4.11 Значение целевой функции в вершине (x1 = 0, x2 = 0, x3 = 0). На рис. 4.12 показана таблица коэффициентов для следующей системы в базисном виде для вершины (x1 = 0, x2 =0, x4 =0).
Рис. 4.12 Значение целевой функции в вершине (x1 = 0, x2 = 0, x4 =0). На рис. 4.13 показана таблица коэффициентов для следующей системы в базисном виде для вершины (x1 = 0, x4 =0, x5 =0).
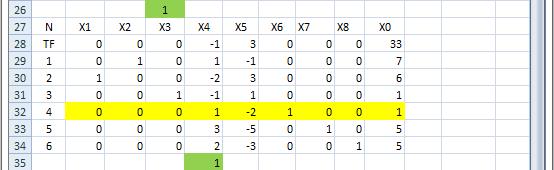
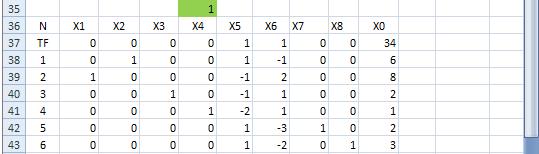
Рис. 4.13 Значение целевой функции в вершине (x1 = 0, x4 = 0, x5 =0). На рис. 4.14 показана таблица коэффициентов для последней системы в базисном виде для вершины (x4 = 0, x5 =0, x6 =0).
Рис. 4.14 Значение целевой функции в вершине (X4 = 0, X5 =0, X6 =0). Как видно из последней таблицы, оптимальным решением задачи является x0000=(1/3, 11/3, 4) и f(x0000)=-46/3 . Варианты заданий для этого примера приведены в приложении 4.3 Алгоритм симплекс-метода: 1. привести задачу к канонической форме: 2. привести систему ограничений к диагональной форме и определить базисные переменные; 3. исключить базисные переменные из целевой функции; 4. построить симплекс-таблицу; 5. проверить найденное д.б.р. на оптимальность: если оно оптимально, то решение закончить; если нет, то идти к пункту 6; 6. вычислить ведущий элемент таблицы; 7. провести симплексное преобразование; 8. построить новое д.б.р. и идти к пункту 5. Если в ведущем столбике нет ни одного строго положительного элемента, то задача не имеет оптимального решения, а целевая функция не ограничена снизу (в задаче на минимум) или не ограничена сверху (в задаче на максимум). Несовместимость системы ограничений (в канонической форме) обнаруживается при построении начального д.б.р. (оно не существует). Симплекс-метод за конечное число итераций либо приводит к оптимальному решению, либо устанавливает неразрешимость задачи (см. пп. 1,2,3). На каждой итерации симплекс-метод сохраняет допустимость базисного решения, т.е. неотрицательность элементов нулевого столбика - следствие правила выбора ведущей строки. На каждой итерации целевая функция убывает (в задаче на минимум) или возрастаем (в задаче на максимум); это свойство нарушается только в случае зацикливания (см. примечания 11,12). В качестве ведущего столбика можно выбирать любой столбик с положительной оценкой (в задаче на минимум), однако максимальность оценки ведущего столбика ведет к сокращению числа итераций (целевая функция быстро убывает).
Приложение 4.1
Варианты заданий для примера 4.1 F(x)=(2,0;0,3), Ограничения: (0,0;0,8;3,8;6,7;9,4;10,2;10,0) F(x)=(2,0;0,3), Ограничения: (0,0;0,8;4,8;8,7;10,5;11;3;11,0) F(x)=(2,0;0,3), Ограничения: (0,0;0,6;3,6;6,5;8,4;10,2;10,0) F(x)=(2,0;0,3), Ограничения: (0,0;0,7;2,7;6,6;8,4;9,2;9,0) F(x)=(2,0;0,3), Ограничения: (0,0;0,7;4,7;7,6;9,5;10,4;11,2;11,0) F(x)=(2,0;0,3), Ограничения: (0,0;0,8;2,8;6,7;9,6;10,5;11,2;11,0) F(x)=(2,0;0,3), Ограничения: (0,0;0,9;3,9;6,8;8,7;9,6;10,3;10,0) F(x)=(2,0;0,3), Ограничения: (0,0;0,9;3,9;6,8;8,7;9,6;10,4;10,0) F(x)=(2,0;0,3), Ограничения: (0,0;0,9;4,9;7,8;9,6;10,310,0) F(x)=(2,0;0,3), Ограничения: (0,0;0,9;4,9;8,8;10,7;11,5;11,0) F(x)=(5,0;0,2), Ограничения: (0,0;0,6;3,6;6,5;8,4;9,3;10,1;10,0) F(x)=(5,0;0,2), Ограничения: (0,0;0,8;3,8;6,7;8,5;10,2;10,0) F(x)=(4,0;0,3), Ограничения: (0,0;0,9;5,9;10,8;13,7;14,6;15,3;15,0) F(x)=(4,0;0,3), Ограничения: (0,0;0,7;4,7;8,6;11,5;12,4;13,2;13,0) F(x)=(4,0;0,3), Ограничения: (0,0;0,9;5,9;10,8;12,7;13,6;14,3;14,0) F(x)=(6,0;0,5), Ограничения: (0,0;0,10;4,10;8,9;10,8;12,6;13,3;13,0) F(x)=(4,0;0.3), Ограничения: (0,0;0,7;5,7;10,6;12,5;13,4;14,2;14,0) F(x)=(4,0;0,5), Ограничения: (0,0;0,10;4,10;8,9;11,7;12,6;14,3;14,0) F(x)=(6,0;0,5), Ограничения: (0,0;0,10;4,10;8,9;11,7;12,6;14,3;14,0) F(x)=(8,0;0,5), Ограничения: (0,0;0,10;4,10;8,9;11,7;12,6;14,3;14,0) F(x)=(3,0;0,5), Ограничения: (0,0;0,10;4,10;8,9;10,8;12,6;13,3;13,0) F(x)=(4,0;0,5), Ограничения: (0,0;0,10;5,10;10,9;12,8;14,3;14,0) F(x)=(2,0;0.5), Ограничения: (0,0;0,10;5,10;10,9;12,8;14,5;14,0) F(x)=(7,0;0,5), Ограничения: (0,0;0,10;5,10;10,9;12,7;13,5;14,2;14,0) F(x)=(7,0;0,5), Ограничения: (0,0;0,10;6,10;9,9;12,6;14,3;14,0) F(x)=(4,0;0,5), Ограничения: (0,0;0,10;6,10;9,9;12,6;14,2;14,0) F(x)=(3,0;0,4), Ограничения: (0,0;0,8;3,8;9,7;12,6;13,5;14,3;14,0) F(x)=(3,0;0,4), Ограничения: (0,0;0,9;4,9;8,8;10,7;13,4;14,2;14,0) F(x)=(3,0;0,4), Ограничения: (0,0;0,10;3,10;9,9;12,8;13,6;14,3;14,0) F(x)=(3,0;0,5), Ограничения: (0,0;0,10;3,10;9,9;12,8;13,5;14,1;14,0) F(x)=(8,0;0,5), Ограничения: (0,0;0,10;3,10;8,9;12,8;13,6;14,3;14,0) F(x)=(8,0;0,5), Ограничения: (0,0;0,8;5,8;10,7;12,6;13,5;14,3;14,0) F(x) = (6,0;0,4); Ограничения: (0,0;0,14;6,14;12,12;18,8;20,4;20,0) F(x) = (6,0;0,4); Ограничения: (0,0;0,14;4,14;12,12;18,8;20,6;22,2;22,0) F(x) = (6,0;0,8); Ограничения: (0,0;0,14;4,14;12,12;18,8;20,6;22,2;22,0) F(x) = (6,0;0,8); Ограничения: (0,0;0,16;4,16;12,14;16,12;20,8;22,4;22,0) F(x) = (6,0;0,4); Ограничения: (0,0;0,16;4,16;12,14;16,12;20,8;22,4;22,0) F(x) = (8,0;0,6); Ограничения: (0,0;0,16;4,16;12,14;16,12;20,8;22,4;22,0) F(x) = (6,0;0,8); Ограничения: (0,0;0,16;4,16;12,14;16,12;20,8;22,4;22,0) F(x) = (6,0;0,10); Ограничения: (0,0;0,16;4,16;12,14;16,12;20,8;22,4;22,0) F(x) = (4,0;0,10); Ограничения: (0,0;0,16;4,16;12,14;16,12;20,8;22,4;22,0) F(x) = (10,0;0,4); Ограничения: (0,0;0,16;4,16;12,14;16,12;20,8;22,4;22,0) F(x) = (10,0;0,4); Ограничения: (0,0;0,16;6,16;12,14;16,12;20,8;22,4;22,0) F(x) = (8,0;0,10); Ограничения: (0,0;0,16;6,16;12,14;16,12;20,8;22,4;22,0) F(x) = (6,0;0,4); Ограничения: (0,0;0,16;6,16;12,14;16,12;20,8;22,4;22,0) F(x) = (4,0;0,6); Ограничения: (0,0;0,16;6,16;12,14;16,12;20,8;22,4;22,0) F(x) = (4,0;0,8); Ограничения: (0,0;0,16;6,16;12,14;16,12;20,8;22,4;22,0) F(x) = (4,0;0,10); Ограничения: (0,0;0,16;6,16;12,14;16,12;20,8;22,4;22,0)
F(x) = (4,0;0,10); Ограничения: (0,0;0,16;8,16;14,14;18,12;20,8;22,2;22,0) F(x) = (6,0;0,8); Ограничения: (0,0;0,16;8,16;14,14;18,12;20,8;22,2;22,0) F(x) = (8,0;0,6); Ограничения: (0,0;0,16;8,16;14,14;18,12;20,8;22,2;22,0) F(x) = (8,0;0,4); Ограничения: (0,0;0,16;8,16;14,14;18,12;20,8;22,2;22,0)
Приложение 4.2 Варианты заданий для примера 4.2 f(x) = x1 + 7x2 + 5x3 + 5x4 + 4x5 + 13x6 → min x1 + x4 = 40 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 7x3 + 3x4 + 4x5 + 12x6 → min x1 + x4 = 70 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 7x4 + 4x5 + 15x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 70 xi ≥ 0, i =1,…,6 f(x) = x1 + 5x2 + 5x3 + 3x4 + 4x5 + 11x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 40 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6
f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 18x6 → min x1 + x4 = 50 x2 + x5 = 30 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 7x3 + 3x4 + 4x5 + 10x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 60 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 19x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 90 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = 2x1 + 11x2 + 5x3 + 7x4 + 4x5 + 14x6 → min x1 + x4 = 40 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 9x3 + 3x4 + 5x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 40 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 12x6 → min x1 + x4 = 50 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 9x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 70 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 5x4 + 4x5 + 14x6 → min x1 + x4 = 40 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = 3x1 + 9x2 + 5x3 + 3x4 + 4x5 + 12x6 → min x1 + x4 = 40 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 7x4 + 4x5 + 14x6 → min x1 + x4 = 80 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 4x4 + 4x5 + 14x6 → min x1 + x4 = 60 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 11x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 90 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 8x5 + 14x6 → min x1 + x4 = 80 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = 2x1 + 9x2 + 3x3 + 3x4 + 4x5 + 14x6 → min x1 + x4 = 40 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 5x4 + 4x5 + 14x6 → min x1 + x4 = 60 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 19x6 → min x1 + x4 = 90 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 7x4 + 4x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 20 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 14x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 70 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 13x4 + 4x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 70 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 15x3 + 3x4 + 4x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 90 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 9x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 80 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 10x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 9x5 + 14x6 → min x1 + x4 = 50 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 7x4 + 4x5 + 14x6 → min x1 + x4 = 50 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 8x4 + 4x5 + 14x6 → min x1 + x4 = 80 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = 3x1 + 9x2 + 6x3 + 3x4 + 4x5 + 14x6 → min x1 + x4 = 50 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 7x4 + 4x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 70 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 5x2 + 5x3 + 8x4 + 4x5 + 14x6 → min x1 + x4 = 70 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 7x2 + 5x3 + 5x4 + 4x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + x4 = 20 x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2 x4 = 40 x2 + x5 = 50 2x3 + x6 = 30 x4 + 5x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2 x4 = 20 x2 + x5 = 50 2x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2x4 = 20 x2 + x5 = 50 2x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2x4 = 20 x2 + x5 = 50 2x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2x4 = 20 x2 + x5 = 50 2x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2x4 = 20 x2 + x5 = 50 2x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2x4 = 20 x2 + x5 = 50 2x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2x4 = 20 x2 + x5 = 50 2x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2x4 = 20 x2 + x5 = 50 2x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2x4 = 20 x2 + x5 = 50 2x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 7x2 + 5x3 + 3x4 + 4x5 + 13x6 → min x1 + 2x4 = 40 x2 + x5 = 50 2x3 + x6 = 40 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 7x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2x4 = 50 x2 + x5 = 50 2x3 + x6 = 60 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 7x2 + 5x3 + 5x4 + 4x5 + 13x6 → min x1 + 2x4 = 40 x2 + x5 = 50 2x3 + x6 = 60 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 7x2 + 5x3 + 3x4 + 4x5 + 15x6 → min x1 + 3 x4 = 40 3x2 + x5 = 50 x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 11x2 + 5x3 + 5x4 + 4x5 + 15x6 → min x1 + 3x4 = 30 x2 + x5 = 50 3x3 + x6 = 40 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 11x2 + 5x3 + 5x4 + 9x5 + 13x6 → min x1 + 4x4 = 20 x2 + x5 = 50 3x3 + x6 = 30 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6 f(x) = x1 + 11x2 + 5x3 + 3x4 + 4x5 + 14x6 → min x1 + 2x4 = 30 x2 + x5 = 50 3x3 + x6 = 60 x4 + x5 + x6 = 60 xi ≥ 0, i =1,…,6
Приложение 4.3 Варианты заданий для примера 4.3 F (x) = x1 - 2x2 - 3x3 → min 2x1 - x2 + 3x3 + x4 = 1 - 4x1 + 2x2 - 4x3 + x5 = 2 3x1 + x3 + x6 = 5 x1,…, x6 ≥ 0 F (x) = 2x1 - x2 - 3x3 → min 2x1 - x2 + x3 + x4 = 1 - 4x1 + 2x2 - 4x3 + x5 = 2 3x1 + 5x3 + x6 = 5 x1,…, x6 ≥ 0 F (x) = x1 - 3x2 - 3x3 → min 2x1 - x2 + 2x3 + x4 = 1 - 4x1 + 2x2 - 4x3 + x5 = 2 3x1 + x3 + x6 = 5 x1,…, x6 ≥ 0 F (x) = x1 - x2 - 4x3 → min 2x1 - x2 + 2x3 + x4 = 1 - 4x1 + 2x2 - 3x3 + x5 = 3 3x1 + x3 + x6 = 5 x1,…, x6 ≥ 0 F (x) = x1 - 2x2 - 5x3 → min 2x1 - 2x2 + x3 + x4 = 1 - 4x1 + 2x2 - 3x3 + x5 = 2 3x1 + x3 + x6 = 6 x1,…, x6 ≥ 0 F (x) = x1 - 4x2 - 3x3 → min 2x1 - 2x2 + 5x3 + x4 = 1 - 4x1 + 2x2 - 4x3 + x5 = 2 3x1 + x3 + x6 = 5 x1,…, x6 ≥ 0
F (x) = x1 - x2 - 3x3 → min 2x1 - x2 + 3x3 + x4 = 3 - 4x1 + 2x2 - 4x3 + x5 = 2 3x1 + x3 + x6 = 5 x1,…, x6 ≥ 0 F (x) = x1 - 4x2 - 3x3 → min 2x1 - x2 + x3 + x4 = 2 - 4x1 + 2x2 - x3 + x5 = 2 3x1 + 2x3 + x6 = 5 x1,…, x6 ≥ 0 F (x) = x1 - 3x2 - 3x3 → min 2x
Поиск по сайту: |
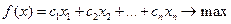
 (4.1)
(4.1) . Это - стандартная форма задачи ЛП. В общем случае ограничения могут иметь знак „
. Это - стандартная форма задачи ЛП. В общем случае ограничения могут иметь знак „  " или „=". Однако, умножая неравенство на -1 и
" или „=". Однако, умножая неравенство на -1 и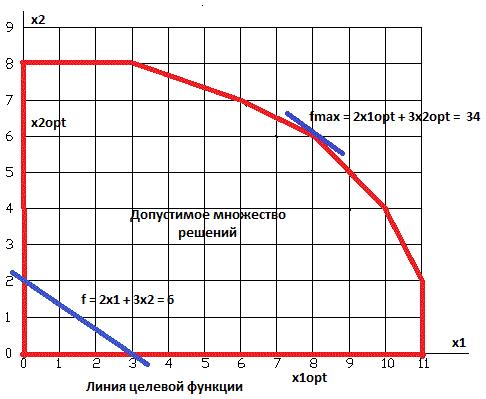
 (4.2)
(4.2)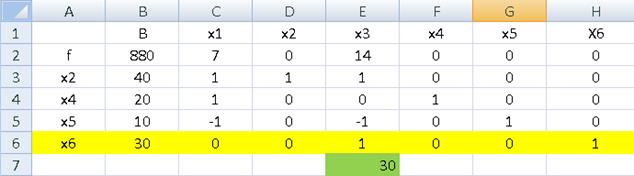
 , получим каноническую форму (слабые переменные на целевую функцию не влияют):
, получим каноническую форму (слабые переменные на целевую функцию не влияют):