 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Принцип сохранения энергии
Слово энергия происходит от индоевропейского корня uerg:
эрг – эргон – энéргейя
Поскольку древние греки связывали сущность любого явления с чем-то неизменным в нем, с идеей, то и под эргоном они понимали вещь в смысле ее полного осуществления, вещь, ставшую наличной. Следовательно, энéргейя – это действие, которое полностью осуществляет эту вещь, выводит ее в наличное бытие. У Аристотеля мера действия – тоже не столько работа или продукт действия, сколько приближение к полноте осуществления. Поэтому, энéргейя – это завершение осуществления формы-сущности какой-либо вещи. Кроме понятия энéргейи он вводит также понятие дюнамис (δύναμις) – сил, способных к такому осуществлению. Римляне понимали эргон уже как результат действия (actio), а энергию как действительность (actus), достигнутую вследствие действия соответствующей причины (causa). Causa → actus. Таким образом, между причиной и следствием устанавливается временная связь. В схоластике Средних веков дюнамис и энéргейю Аристотеля свели к категориям возможности (potentia) и действительности (actus). Действительность – это то, что наступает в порядке следствия в результате действия причины и требует определенного усилия или работы. Поэтому, энергия стала пониматься как деятельная сила, активность. В естествознании XVI-XVII веков соотношение причины и следствия уже выступает в качестве теоретического принципа. Лейбниц трактует его следующим образом: Позже, в 1807 году, Юнг назвал эту величину энергией. В самом деле,
Работа силы дается изменением величины Дальнейшие наблюдения за реальными движениями тел показали, что: 1) 2) для консервативных сил, работа которых не зависит от формы траектории, целесообразно ввести понятие потенциальной энергии 3) Силы трения или сопротивления движению приводят к уменьшению В 1840-х годах обратили внимание на превращение различных форм движения в теплоту. Майер выдвинул идею поиска эквивалентов, т.е. количественных соотношений между явлениями природы. Так как причина равна действию, то следствие возникает за счет определенной затраты причины, которую можно выразить в числах. Майер вычислил механический эквивалент теплоты (1 кал ≈ 4,2 Дж) следующим образом: Пусть Имея данные о Джоуль и Ленц измерили электрический эквивалент теплоты (0,24 кал = Гесс установил принцип, согласно которому тепловой эффект химической реакции зависит только от начального и конечного состояния веществ и не зависит от промежуточных стадий. Например, получение Na2SO4 из H2SO4 и NaOH (в растворе) может быть осуществлено в процессе, имеющем одну стадию: 2 NaOH + H2SO4 = Na2SO4 + 2 H2O + 131,4 кДж; или же в двухстадийном процессе: а) NaOH + H2SO4 = NaHSO4 + H2O + 61,7 кДж, б) NaHSO4 + NaOH = Na2SO4 + H2O + 69,7 кДж. Как видно, суммарный тепловой эффект двухстадийного процесса оказывается таким же, как и тепловой эффект одностадийного. После того, как в науке утвердилось представление о теплоте как беспорядочном и непрерывном движении атомов и молекул, закон сохранения энергии приобрел статус общефизического принципа: Энергия не возникает из ничего и не уничтожается бесследно, различные ее Таким образом, энергия есть общая мера различных форм движения и соответствующих им взаимодействий. Вводя механическую, тепловую, электрическую, ядерную и т.д. энергию, можно изучать как известные, так и новые явления природы. Пример. Взаимосвязь массы и энергии в релятивистской механике. Выражение для релятивистской массы допускает разложение в ряд:
Тогда Если тело изолировано, то его полная энергия
Статистическое истолкование Классическая термодинамика изучает объекты макромира без рассмотрения их атомно-молекулярной структуры. Но так как эти объекты на самом деле состоят из множества структурных элементов (в 1 моле – 6,02∙1023), то их можно считать системами большого числа частиц и применять к ним методы математической статистики. Классический вариант статистического подхода в физике сложился во второй половине XIX века в работах Максвелла, Больцмана и Гиббса. Этот подход заключается в том, что характеристики движения отдельных частиц усредняются и связываются с термодинамическими параметрами системы как целого. Первоначально этот подход опирался на молекулярно-кинетическую теорию вещества. Согласно этой теории все тела состоят из атомов, молекул и ионов, находящихся в непрерывном хаотическом движении. Это механическое движение было названо тепловым, так как объясняло наблюдаемые тепловые явления. Наиболее простой и удобной теоретической моделью оказался идеальный газ. По-существу, это система материальных точек-молекул, участвующих в тепловом движении. В состоянии термодинамического равновесия и отсутствия внешнего поля все направления движения равновероятны и скорости молекул могут иметь любые значения от 0 до ∞. В 1860 году Максвелл теоретически показал, что в этом случае в результате столкновений (теплового движения) в идеальном газе устанавливается стационарное распределение молекул по скоростям в виде:
Тогда для конечного интервала
Очевидно, что не все значения скоростей равновероятны (так как
Большинство молекул будут иметь скорости в средней части графика Средняя арифметическая скорость
Рисунок 9
Таким образом, даже в такой простой модели идеального газа характеристики движения отдельной частицы несущественны. Одно и то же состояние системы, определяемое термодинамическим параметром Т, может осуществляться множеством способов распределения отдельных частиц по скоростям теплового движения. Частицы могут иметь любые значения Пример. При упорядоченном движении тела энергия системы его молекул W распределена между ними малым числом способов, так как бóльшая ее часть сконцентрирована в виде энергии кинетической После остановки тела в результате действия силы трения, Итак, необратимость тепловых процессов имеет вероятностный характер. Больцман (1872 г.) предложил связать энтропию и вероятность. Впоследствии была установлена формула Таким образом, статистическое истолкование II начала термодинамики заключается в том, что термодинамическая вероятность состояния изолированной системы не может уменьшаться при любых процессах в ней. Следствия статистического истолкования. 1) Границы применимости II начала. В случае малого числа частиц в системе II начало становится неприменимым, так как термодинамические вероятности состояний становятся практически равными, и хаотичность теплового движения может вызвать обратимость процесса. Пример. Две частицы в объеме, разделенном проницаемой перегородкой на две части I и II. Частицы могут свободно переходить из одной части в другую. Возможны три состояния такой системы:
I II Г1 > Г2 , Г3 , значит, более вероятен процесс 2) → 1) или 3) → 1). Однако, как показывает опыт, за большой промежуток времени 2) «Тепловая смерть» Вселенной. Распространение II начала на всю Вселенную, как это сделал Клаузиус, приводит к выводу о переходе всех видов энергии в тепловую и равномерном ее распределении по веществу. При этом 3) Поскольку время выражает порядок следования явлений, то факт их необратимости в макромире позволяет обосновать факт необратимости времени. Таким образом, классическая физика подтверждает устойчивость окружающего мира.
Поиск по сайту: |

 Werk (нем.)
Werk (нем.) uerg Work (англ.) дело, творение, работа
uerg Work (англ.) дело, творение, работа
 εργον (греч.)
εργον (греч.) ενέργεια
ενέργεια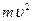 , где
, где  – масса тела,
– масса тела, 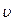 – его скорость. Лейбниц даже предположил, что
– его скорость. Лейбниц даже предположил, что 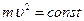 .
.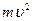 может быть мерой действия силы, если это действие охарактеризовать работой:
может быть мерой действия силы, если это действие охарактеризовать работой: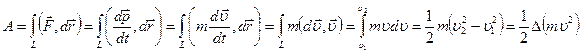 .
. была названа кинетической энергией. Она определена с точностью до постоянного слагаемого
была названа кинетической энергией. Она определена с точностью до постоянного слагаемого 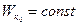 , которое находится из условий конкретной задачи. Таким образом, работа силы равна изменению кинетической энергии тела
, которое находится из условий конкретной задачи. Таким образом, работа силы равна изменению кинетической энергии тела 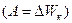 ;
;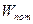 , зависящей только от положения тела, так что
, зависящей только от положения тела, так что  . Тогда полная механическая энергия будет сохраняться, т.е.
. Тогда полная механическая энергия будет сохраняться, т.е. 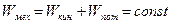 . Действительно,
. Действительно,  .
.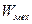 , и закон сохранения механической энергии имеет ограниченное применение.
, и закон сохранения механической энергии имеет ограниченное применение.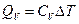 – теплота, переданная газу при
– теплота, переданная газу при 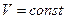 ; в этом процессе механическая работа газа
; в этом процессе механическая работа газа 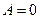 . Пусть далее
. Пусть далее 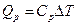 – теплота, переданная этому же газу при
– теплота, переданная этому же газу при 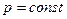 ; работа его расширения в этом процессе
; работа его расширения в этом процессе  . Следовательно, часть теплоты,
. Следовательно, часть теплоты, 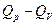 , превращается в механическую работу:
, превращается в механическую работу: 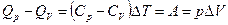 , где
, где  измеряется в калориях (кал), а А – в джоулях (Дж).
измеряется в калориях (кал), а А – в джоулях (Дж).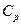 и
и 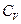 , можно вычислить эквивалент. Джоуль определил его экспериментально, измеряя изменение температуры
, можно вычислить эквивалент. Джоуль определил его экспериментально, измеряя изменение температуры 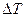 вследствие действия трения при движении тела.
вследствие действия трения при движении тела.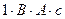 ), используя установленный ими закон: теплота, выделенная электрическим током,
), используя установленный ими закон: теплота, выделенная электрическим током, 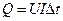 , где U – напряжение, I – сила тока,
, где U – напряжение, I – сила тока, 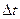 – время.
– время.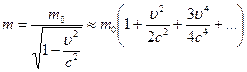 , причем если
, причем если 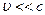 , можно ограничиться только двумя первыми слагаемыми. Здесь
, можно ограничиться только двумя первыми слагаемыми. Здесь  – масса покоя тела,
– масса покоя тела, 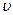 – его скорость, с – скорость света в вакууме.
– его скорость, с – скорость света в вакууме. ; где
; где  – энергия покоя.
– энергия покоя. ; принцип относительности требует, чтобы этот закон выполнялся во всех системах отсчета, т.е. и при
; принцип относительности требует, чтобы этот закон выполнялся во всех системах отсчета, т.е. и при 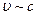 ; тогда
; тогда  . Такой же результат получается и для других видов энергии, поэтому между массой и энергией существует универсальное соотношение:
. Такой же результат получается и для других видов энергии, поэтому между массой и энергией существует универсальное соотношение: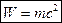 – формула Эйнштейна.
– формула Эйнштейна. , где
, где 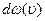 – вероятность того, что модуль скорости любой молекулы заключен в интервале
– вероятность того, что модуль скорости любой молекулы заключен в интервале 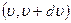 ,
,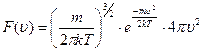 – функция распределения Максвелла, m – масса молекулы, Т – температура, k – постоянная Больцмана.
– функция распределения Максвелла, m – масса молекулы, Т – температура, k – постоянная Больцмана.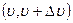 вероятность равна:
вероятность равна: .
. будут различны для одного и того же
будут различны для одного и того же 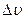 ).
).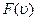 , вблизи
, вблизи 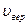 – наиболее вероятной скорости (значение
– наиболее вероятной скорости (значение 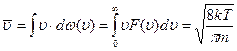 – связана с термодинамическим параметром Т.
– связана с термодинамическим параметром Т.
 – средняя скорость будет иметь одно определенное значение, связанное с Т. Очевидно также, что более вероятно такое состояние системы, которое осуществляется бóльшим числом способов, и процесс перехода в него будет более вероятен.
– средняя скорость будет иметь одно определенное значение, связанное с Т. Очевидно также, что более вероятно такое состояние системы, которое осуществляется бóльшим числом способов, и процесс перехода в него будет более вероятен.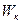 , т.е.
, т.е. 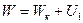 , где
, где  – внутренняя энергия теплового движения.
– внутренняя энергия теплового движения.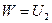 , причем
, причем  , молекулы движутся теперь неупорядоченно, и поэтому энергия распределяется между ними бóльшим числом способов. Следовательно, переход механической энергии в теплоту более вероятен, чем обратный переход.
, молекулы движутся теперь неупорядоченно, и поэтому энергия распределяется между ними бóльшим числом способов. Следовательно, переход механической энергии в теплоту более вероятен, чем обратный переход. , где Г – термодинамическая вероятность состояния системы, т.е. число способов распределения частиц, осуществляющих данное состояние. Тогда, если процесс обратим, то все состояния равновероятны и
, где Г – термодинамическая вероятность состояния системы, т.е. число способов распределения частиц, осуществляющих данное состояние. Тогда, если процесс обратим, то все состояния равновероятны и  ,
, 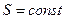 , а если необратим, то Г ↑ и S ↑ => для изолированной системы
, а если необратим, то Г ↑ и S ↑ => для изолированной системы  .
. 1) Г1 = 2
1) Г1 = 2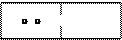 2) Г2 = 1
2) Г2 = 1 3) Г3 = 1
3) Г3 = 1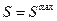 . Прекратятся все процессы, кроме теплового движения, и наступит тепловое равновесие. Однако нет оснований считать Вселенную изолированной термодинамической системой. Поэтому II начало, по-видимому, неприменимо к системам с бесконечным числом частиц.
. Прекратятся все процессы, кроме теплового движения, и наступит тепловое равновесие. Однако нет оснований считать Вселенную изолированной термодинамической системой. Поэтому II начало, по-видимому, неприменимо к системам с бесконечным числом частиц.