 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные положения квантовой механики
Исследования атомных и субатомных явлений в ХХ веке показали, что свойства микрообъектов существенно отличаются от привычных свойств макроскопических тел и что для их понимания нельзя пользоваться классическими физическими теориями. Уже в экспериментах начала ХХ века выявились, прежде всего, следующие две стороны физической реальности микромира, непонятные с точки зрения классической механики. 1) Ряд механических величин, например, энергия или момент импульса микрочастицы, могут иметь только определенные дискретные значения W1, W2, …, Wn, в то время как в классической механике эти величины всегда имели непрерывное множество в принципе любых значений. 2) Существует взаимодействие между объектом измерения и измерительным прибором, которое приводит к тому, что при измерении одной физической характеристики может возникнуть изменение другой, измеренной ранее. Следовательно, мы не можем одновременно точно знать все характеристики микрообъекта. Классическая теория предполагает, что взаимодействие объекта и прибора в принципе можно исключить. Таким образом, классическая механика пригодна, по-видимому, для рассмотрения движения тел большой массы, а в области малых масштабов необходима более общая механика. Квантовая механика изучает движение частиц в области микромира на расстояниях менее 10-8 м, т.е. движение атомов, молекул, элементарных частиц и частиц кристаллов. Предшественницей квантовой механики была квантовая теория света Планка и Эйнштейна. Свет, да и вообще любое электромагнитное излучение имеет как волновые, так и квантовые свойства, проявляющиеся в разной степени. Волновые свойства более заметны для низкочастотного диапазона (радиоволны, инфракрасный (ИК) и видимый свет), а квантовые – для высокочастотного (ультрафиолет (УФ), рентген, γ-лучи). Вещество – тоже материальный объект, как и электромагнитное поле, и поэтому естественно предположить наличие волновых свойств у вещества, проявляющихся в разной степени. Кванты света или фотоны в теории Эйнштейна, кроме энергии Поскольку импульс характерен, прежде всего, для движущихся тел ( Любой движущейся частице вещества можно поставить в соответствие волну с длиной Так как h = 6,62∙10-34 Дж∙с, то λ достаточно велика только у частиц малой массы. Поэтому волновые свойства движущихся микрочастиц уверенно наблюдаются, а макрообъекты их не проявляют. Например, при скорости Никакие известные виды волн не подходят для описания природы волн де Бройля. Эти волны имеют смысл волн вероятности. Плоская волна свободной частицы соответствует равной вероятности ее нахождения в любом месте пространства. Взаимодействие частицы с кристаллической решеткой трактуется как рассеяние этой волны на трехмерной структуре, и в результате этого вероятность попадания частицы в разные точки становится неодинаковой. Волновая природа движения микрочастиц приводит к тому, что если к ним применяются понятия классической механики, например, координаты или импульса, то возникают неустранимые неточности при определении соответствующих величин. Они выражаются соотношениями неопределенностей Гейзенберга (1927). Наибольшее практическое значение имеют два соотношения. 1) Для неопределенностей координат и импульсов:
т.е. если х известно с точностью Δх ( то импульс рх можно измерить только с точностью до 2) Для неопределенностей энергии и времени:
Для описания движения микрочастиц Шрёдингер (1926) предложил уравнение:
где Решением этого уравнения при заданных начальных и граничных условиях является волновая функция Современная теория атома использует квантовую механику. Решение уравнения Шрёдингера для электронов в поле ядра дает соответствующие параметры атомов и атомных систем. Результаты теории: 1) физические величины, характеризующие свойства атома, имеют дискретные значения (квантованы); 2) эти значения определяются в общем случае четырьмя квантовыми числами; 3) электроны следует представлять в виде облака отрицательного заряда различной формы, радиус орбиты представляет собой наиболее вероятное положение электрона относительно ядра. Одинаковые частицы в микромире принципиально неразличимы (если поменять местами два электрона в атоме, то ничего не изменится). Основываясь на этом факте, Паули (1925) выдвинул принцип:
Поиск по сайту: |
 , имеют также импульс
, имеют также импульс  .
. ), де Бройль (1924) выдвинул следующую гипотезу:
), де Бройль (1924) выдвинул следующую гипотезу: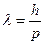 , где
, где  – импульс частицы.
– импульс частицы.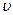 ~ 106 м/с длина волны электрона λе ~ 7∙10-10 м. Следовательно, его дифракцию можно наблюдать практически на любой кристаллической структуре с периодом d ~ 10-10 м. Длина волны пули массой 10 г, летящей со скоростью 300 м/с, составляет примерно 2∙10-34 м, и ее дифракцию пронаблюдать нельзя, так как такие маленькие структуры экспериментально недоступны.
~ 106 м/с длина волны электрона λе ~ 7∙10-10 м. Следовательно, его дифракцию можно наблюдать практически на любой кристаллической структуре с периодом d ~ 10-10 м. Длина волны пули массой 10 г, летящей со скоростью 300 м/с, составляет примерно 2∙10-34 м, и ее дифракцию пронаблюдать нельзя, так как такие маленькие структуры экспериментально недоступны.
 ),
), .
. ; т.е. если частица пребывает в течение времени Δt в состоянии с энергией W, то эта энергия в принципе может быть определена только с точностью до ΔW, и, наоборот, энергия может быть определена точно (ΔW = 0) только для бесконечно большого промежутка времени (Δt →∞).
; т.е. если частица пребывает в течение времени Δt в состоянии с энергией W, то эта энергия в принципе может быть определена только с точностью до ΔW, и, наоборот, энергия может быть определена точно (ΔW = 0) только для бесконечно большого промежутка времени (Δt →∞). ,
, ,
, 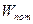 – потенциальная энергия частицы, m – ее масса,
– потенциальная энергия частицы, m – ее масса,  .
. . Она характеризует вероятность нахождения частицы в точке
. Она характеризует вероятность нахождения частицы в точке  в момент времени t и позволяет найти наблюдаемые значения ее параметров.
в момент времени t и позволяет найти наблюдаемые значения ее параметров.