 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Законы сохранения механических величин
Механика ставит перед собой две основные задачи: 1. Изучение различных движений и обобщение полученных результатов в виде законов движения. 2. Поиск общих свойств, присущих любой механической системе независимо от вида взаимодействий между ее телами. Решение первой задачи привело к установлению динамических законов, которые позволяют в принципе вычислить положение тела в любой момент времени при его конкретном движении. Например, для того чтобы определить координату материальной точки х в любой момент времени, надо проинтегрировать уравнение 2-го закона Ньютона 1) законы действия сил могут быть неизвестны; 2) уравнения могут не иметь методов решения; 3) существуют задачи, в которых нет смысла рассматривать движение отдельных тел системы (например, молекул газа). В этих случаях актуальна вторая задача механики. Ее решение привело к обнаружению законов сохранения энергии, импульса и момента импульса. Эти законы позволяют рассмотреть общие свойства движения без решения уравнений и детальной информации о развитии процессов во времени. Математически они сводятся к постоянству численного значения определенной физической величины или комбинации величин. Поэтому фактически они дают дополнительные и, как правило, более простые уравнения, чем уравнения движения, облегчающие решение задачи. Закон сохранения механической энергии Однородность времени означает, что если в любые два момента времени все тела замкнутой системы поставить в одинаковые условия, то, начиная с этих моментов времени, все явления в ней будут протекать одинаково. Пример. На работу механических часов влияют различные факторы, зависящие от времени. Поэтому, вообще говоря, время для часов неоднородно. Например, период колебаний маятника будет меняться вследствие изменения атмосферного давления, влажности воздуха, времени суток и т.п. Однако, как правило, притяжение к Земле является основным фактором, обеспечивающим колебание маятника. Если пренебречь всеми прочими влияниями и считать систему часов с маятником замкнутой системой, время для них будет однородным. В конечном счете, это позволяет независимо от других явлений измерять время часами. Закон сохранения импульса Однородность пространства означает, что если замкнутую систему, как целое, перенести из одного места в другое, то это не отразится на ходе всех последующих явлений в ней.
Пример. Падение камня на Землю.
Рисунок 7
Вдоль оси х на камень действует сила тяжести Закон сохранения момента импульса Изотропность пространства означает, что если замкнутую систему, как целое, повернуть на любой угол, то это не отразится на ходе всех последующих явлений в ней. Пример. Вращение волчка в плоскости ху под действием постоянного момента сил
Рисунок 8
В рамках механики законы сохранения являются следствиями законов Ньютона, однако, как показывает опыт, если расширить понятие энергии, импульса и момента импульса, законы их сохранения становятся универсальными принципами для всей физики и естествознания. Расширение понятия энергии за пределы механики привело к универсальному закону сохранения полной энергии для изолированных систем: W = const. В таком виде он уже не может быть выведен из законов Ньютона, а должен рассматриваться как наиболее широкое обобщение опытных фактов. Аналогично, законы сохранения импульса и момента импульса тоже оказываются применимыми для любых материальных объектов. Например, взаимодействие электромагнитных волн с веществом подчиняется закону сохранения импульса, если наблюдаемые при этом свойства волн описать при помощи обобщенного понятия импульса. Соответственно, свойства однородности и изотропности пространства и времени следует при этом понимать уже не только в механическом смысле, и они связаны с новыми аспектами движения материальных объектов.
Поиск по сайту: |
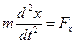 . Если известен закон действия силы Fx и положение точки в начальный момент времени, т.е.
. Если известен закон действия силы Fx и положение точки в начальный момент времени, т.е.  то эта задача может быть решена. Трудности возникают, главным образом, в следующих случаях:
то эта задача может быть решена. Трудности возникают, главным образом, в следующих случаях: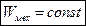 , где
, где  , для замкнутой консервативной системы N тел можно получить из 2-го закона Ньютона, если при этом учесть свойство однородности времени.
, для замкнутой консервативной системы N тел можно получить из 2-го закона Ньютона, если при этом учесть свойство однородности времени. , где
, где  , для замкнутой механической системы N тел можно получить из 2-го закона Ньютона, если при этом учесть свойство однородности пространства.
, для замкнутой механической системы N тел можно получить из 2-го закона Ньютона, если при этом учесть свойство однородности пространства.
 , где m – масса камня,
, где m – масса камня,  – ускорение свободного падения. По 2-му закону Ньютона
– ускорение свободного падения. По 2-му закону Ньютона  . Следовательно,
. Следовательно,  . Пространство для камня вдоль оси х неоднородно, т.к. начальные положения х1 и х2 камня неэквивалентны в отношении последующего движения. Вдоль осей у и z силы не действуют,
. Пространство для камня вдоль оси х неоднородно, т.к. начальные положения х1 и х2 камня неэквивалентны в отношении последующего движения. Вдоль осей у и z силы не действуют,  , следовательно,
, следовательно, 
 . Пространство вдоль этих осей однородно, т.к. в отношении последующего движения камня ничего не изменится, если точку его бросания перенести по оси z (из z1 в z2) или по оси у.
. Пространство вдоль этих осей однородно, т.к. в отношении последующего движения камня ничего не изменится, если точку его бросания перенести по оси z (из z1 в z2) или по оси у. , где
, где 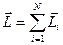 , для замкнутой механической системы N тел можно получить из 2-го закона Ньютона, если при этом учесть свойство изотропности пространства.
, для замкнутой механической системы N тел можно получить из 2-го закона Ньютона, если при этом учесть свойство изотропности пространства. . Согласно уравнению динамики вращательного движения
. Согласно уравнению динамики вращательного движения  ,
,  . Следовательно,
. Следовательно, 
 ,
,  . Вдоль осей x и y пространство изотропно, т.к. поворот волчка на любой угол вокруг этих осей никак не повлияет на характер дальнейшего движения. Вдоль оси z пространство неизотропно, т.к., если в некоторый момент времени повернуть волчок на угол α относительно этой оси, его новое положение не будет эквивалентно положению до поворота в отношении последующего движения.
. Вдоль осей x и y пространство изотропно, т.к. поворот волчка на любой угол вокруг этих осей никак не повлияет на характер дальнейшего движения. Вдоль оси z пространство неизотропно, т.к., если в некоторый момент времени повернуть волчок на угол α относительно этой оси, его новое положение не будет эквивалентно положению до поворота в отношении последующего движения.