 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Поняття дробу. Рівність дробів. Основна властивість дробів. Скорочення дробів та їх зведення до спільного знаменника. Нескоротні дроби.
2. Для виконання поставлених завдань введемо означення понять, які відносяться до нової числової множини. Означення: пара чисел (m;n) або символ Знаменник дробу показує на скільки рівних частин поділено величину, а чисельник дробу - скільки таких рівних частин взято. Означення: Дроби, що позначають одне і те ж саме дробове число, називають рівносильними або еквівалентними. Наприклад, дробове число Означення: два дроби Символічно це означення можна записати так: Сформулюємо та доведемо теорему, яку в математиці називають основною властивістю дробів. Теорема:якщо чисельник і знаменник дробу помножити чи поділити на довільне натуральне число, то дістанемо дріб, що дорівнює даному. Доведення. Розглянемо дріб Виявляється, що основна властивість дробів знайшла широке застосування при виконанні таких операцій над дробами як скорочення дробів і зведення дробів до спільного знаменника. Означення: скороченням дробу називається операція ділення чисельника і знаменника дробу на їхні спільні дільники, в результаті якої дріб замінюється рівносильним йому дробом з меншими числами. Означення: зведенням дробів до спільного знаменника називається операція множення чисельника і знаменника на одне і те ж саме, відмінне від нуля число, в результаті якої даний дріб замінюється рівносильним йому, але з вказаним знаменником. Означення: якщо чисельник дробу менший за знаменник, то дріб називають правильним. Якщо чисельник дробу більший за знаменник або дорівнює йому, то дріб називають неправильним. Означення: дріб називають нескоротним, якщо найбільший спільний дільник чисельника і знаменника дорівнює 1. Прикладом правильних дробів серед наступних
Поиск по сайту: |
 , де m і n – натуральні числа, називається звичайним дробом. Число, яке стоїть над рискою, називається чисельником, а число, яке стоїть під рискою, - знаменником дробу.
, де m і n – натуральні числа, називається звичайним дробом. Число, яке стоїть над рискою, називається чисельником, а число, яке стоїть під рискою, - знаменником дробу. можна позначати 1,
можна позначати 1,  ,
,  ,
,  ,...,
,...,  ,..., а дробове число -
,..., а дробове число -  можна позначити:
можна позначити:  ,
,  , ... ,
, ... ,  , …
, …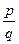 називають рівними, якщо виконується рівність mq=np.
називають рівними, якщо виконується рівність mq=np. .
. чисельник і знаменник на m. Одержимо
чисельник і знаменник на m. Одержимо  . Як показати, що
. Як показати, що 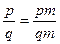 ? – згідно означення про рівні дроби, а це дійсно так, бо p(qm)=q(pm), бо p, q і m ÎN, для яких p(qm)=q(pm), адже справедливі переставний і сполучний закони множення. Аналогічно можна довести і другу частину теореми.
? – згідно означення про рівні дроби, а це дійсно так, бо p(qm)=q(pm), бо p, q і m ÎN, для яких p(qm)=q(pm), адже справедливі переставний і сполучний закони множення. Аналогічно можна довести і другу частину теореми. є перший, другий і четвертий, а неправильним є третій. Прикладом нескоротних дробів є наступні
є перший, другий і четвертий, а неправильним є третій. Прикладом нескоротних дробів є наступні 