 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
МОДУЛЬ У. «РОЗШИРЕННЯ ПОНЯТТЯ ПРО ЧИСЛО».
Змістовний модуль 5.3. «Дійсні числа.». ПЛАН. 1. Необхідність розширення множини раціональних чисел. 2. Додатні ірраціональні числа. Невід’ємні дійсні числа. 3. Відношення порядку на множині дійсних чисел. 4. Додавання і віднімання додатних дійсних чисел. 5. Множення та ділення додатних дійсних чисел. 6. Множина дійсних чисел та її властивості. ЛІТЕРАТУРА:[1] – с. 172-238; [2] – с. 193-246, 325-340; [3] – с. 181-196.
Необхідність розширення множини раціональних чисел. 1. Відомі нам розширення натуральних і цілих чисел були обумовлені потребами практичної діяльності людини та потребами математики. Розширення вказаних числових множин відбувалося за умови виконання певних вимог. Виявилося, що множини раціональних чисел не достатньо як для практичних потреб, так і для потреб математики, бо існують несумірні відрізки та не завжди можна розв'язати рівняння виду х2=а. Як відомо, суть вимірювання довжини відрізка полягає у послідовному відкладанні одного відрізка, який обраний за міру, на іншому відрізкові, який слід виміряти. При цьому можливі два випадки: 1) одиничний відрізок чи його частина відкладаються на заданому відрізкові ціле число раз. У такому разі процес вимірювання закінчується, тобто скінченний, а довжина відрізка виражається невід’ємним раціональним числом. Про такі відрізки говорять, що вони сумірні; 2) ані одиничний відрізок, ані його частина не відкладається на даному відрізку ціле число раз. У цьому випадку процес вимірювання не закінчується, тобто процес вимірювання нескінченний, а довжина заданого відрізка виражається числами якоїсь нової природи. Такі відрізки називають несумірними. Для того, щоб стверджувати, що несумірні відрізки існують, тобто числа нової природи є, доведемо наступну терему. Теорема: діагональ квадрата несумірна з його стороною. Доведення. Для доведення теореми розглянемо квадрат, довжина сторони якого складає 1 одиницю (див. малюнок № 5.2.). За умовою АВ=1, ВС=1. Припустимо, що довжина діагоналі АС дорівнює нескоротному дробу В С
А Д Малюнок № 5.2.
Із доведеної теореми випливає, що, по-перше, існують відрізки, довжина яких не виражається раціональним числом, по-друге, не існує раціонального числа, квадрат якого дорівнює 2, тобто рівняння х2=2 в множині раціональних чисел немає розв'язку. Отже виникає потреба в розширенні множини раціональних чисел, причому повинні виконуватися наступні вимоги: 1) довжина будь-якого відрізка повинна виражатися цим числом; 2) у новій числовій множині завжди повинно мати розв'язок рівняння виду хn=а, де а
Поиск по сайту: |
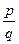 , тобто раціональному числу. За теоремою Піфагора із трикутника АВС маємо: АС2=АВ2+ВС2
, тобто раціональному числу. За теоремою Піфагора із трикутника АВС маємо: АС2=АВ2+ВС2 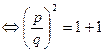 . Тоді (
. Тоді ( 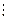 2. Це означає, що число p – парне, тобто p=2p1. Таким чином, 4p12=2q2. Звідси, 2p12=q2, тобто число q – парне і q=2q1. Отже,
2. Це означає, що число p – парне, тобто p=2p1. Таким чином, 4p12=2q2. Звідси, 2p12=q2, тобто число q – парне і q=2q1. Отже, 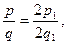 тобто дріб
тобто дріб 

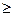 0; 3) множина раціональних чисел повинна входити в нову числову множину.
0; 3) множина раціональних чисел повинна входити в нову числову множину.