 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основна теорема арифметики цілих невід’ємних чисел.
5. Основну теорему арифметики називають також теоремою про існування та єдиність розкладу будь-якого натурального числа на добуток простих множників. Ця теорема використовувалась ще у стародавній Греції, але була сформульована і доведена видатним німецьким математиком К.Гауссом у 1801 році. Теорема: будь-яке, більше за одиницю, натуральне число а, або просте, або може бути однозначно розкладене в добуток простих чисел з точністю до порядку розміщення співмножників. Доведення: доведення складається з двох частин. У першій частині доведемо існування такого розкладу. Якщо аєN і a>1, то можливі два випадки : а) число а – просте, тоді розклад існує; б) число а – складене, тоді воно має найменший простий дільник. Нехай це буде число р1. Виходячи із цього, маємо а
Не виключеним є випадок, коли деякий із множників в розкладі (1) повторюється, а тому в загальному випадку розклад числа на прості множники записують так: У другій частині доведемо єдиність такого розкладу методом від супротивного, припустивши, що існує два різних розклади у вигляді (І), тобто а=р1·р2·р3·…·рк (ІІ) і а=q1·q2·q3·…·qn (III). Врахуємо, що р1<р2<р3<…<рк і q1<q2<q3<…<qn. У даних розкладах рі і qі – різні, але серед них будуть однакові. Для визначеності припустимо, що p1¹q1 i p1<q1. Утворимо нове число b=p1·q2·q3·…·qn (IV). Легко бачити, що число а в записі (1) ділиться націло на p1. Оскільки Доведена теорема є теоретичною основою представлення будь-якого натурального числа у вигляді добутку простих множників. Покажемо це на прикладі такої вправи: „Представити число 1224 у канонічному розкладі, тобто розкласти в добуток простих множників”. Розв’язання:
Поиск по сайту: |
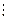 р1 і а=р1b, де bєN, причому число 1<р1< b.
р1 і а=р1b, де bєN, причому число 1<р1< b. Число b може бути або простим, або складеним. Якщо число b – просте, то ми вже можемо представити число а у вигляді добутку двох простих чисел рb, тобто розклад існує. Якщо b – складене число, то воно має простий дільник. Нехай це буде число р2. Виходячи із цього, маємо а
Число b може бути або простим, або складеним. Якщо число b – просте, то ми вже можемо представити число а у вигляді добутку двох простих чисел рb, тобто розклад існує. Якщо b – складене число, то воно має простий дільник. Нехай це буде число р2. Виходячи із цього, маємо а  (І).
(І). (ІІ). Розклад (ІІ) називається канонічним розкладом натурального числа а у добуток простих множників. В цьому розкладі р1, р2, р3,...,рk – прості множники, розміщені в порядку зростання; a1, a2, a3,...,ak– це натуральні числа, які показують, скільки разів повторюється той чи інший множник. Існування доведено.
(ІІ). Розклад (ІІ) називається канонічним розкладом натурального числа а у добуток простих множників. В цьому розкладі р1, р2, р3,...,рk – прості множники, розміщені в порядку зростання; a1, a2, a3,...,ak– це натуральні числа, які показують, скільки разів повторюється той чи інший множник. Існування доведено. , то
, то 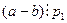 . Використовуючи записи (III) і (IV), винесемо добуток q2·q3·…·qn за дужки: (a-b)=(q1–p1)·q2·q3·...·qn. Ми показали, що вираз
. Використовуючи записи (III) і (IV), винесемо добуток q2·q3·…·qn за дужки: (a-b)=(q1–p1)·q2·q3·...·qn. Ми показали, що вираз  , бо p1¹q1 і ці числа прості. Отже, для того, щоб (q1–p1)
, бо p1¹q1 і ці числа прості. Отже, для того, щоб (q1–p1)