 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
8. Для визначення операції множення на множині натуральних чисел також можна використати два підходи. Згідно з першим, операція множення визначається на основі операції декартового добутку множин. Розглянемо дві скінченні множини А і В такі, що n(А)=а і n(В)=b. Тепер приймемо таке означення: “Добутком натурального числа а на натуральне число b називається число елементів декартового добутку а-елементної множини А на b-елементну множину В, тобто а×b=n(А)●n(В)=n(А´В)”. Для введення іншого означення розглянемо b скінченних еквівалентних між собою множин А1, А2, А3, ... Аb таких, що А1~А2~А3~...~Аb і n(А1)=n(А2)=n(А3)=...=n(Аb)=а. Тепер приймемо таке означення добутку натуральних чисел а і b: “Добутком натурального числа а на натуральне число b, b>1, називають суму b доданків, кожний із яких дорівнює а”. Якщо накласти умову, що множини А1, А2, А3, ... Аb не мають спільних елементів, то а×b=n(А1ÈА2ÈА3È...ÈАb)=n(А1)●n(А2)●n(А3)●...●n(Аb)=а×b. Оскільки доданків не може бути менше, ніж два, то для множення на 0 і на 1 вводяться додаткові означення: “а×0=0 і а×1=а”. Число а називають першим множником, число b – другим множником, число а×b – добутком. Операцію, за допомогою якої знаходять добуток називають множенням. Число а інколи називають множеним, а число b - множником. У жодному із наведених нами означень, які еквівалентні між собою, нічого не говориться про існування та єдиність операції множення та про властивості, яким вона задовольняє. Саме тому слід довести наступні теореми. Теорема 6. (про існування та єдиність добутку): якими б не були цілі невід’ємні числа a і b завжди існує єдине ціле невід’ємне число a×b, яке є їх добутком. Доведення:
b Теорема 7 (переставний або комутативний закон множення): для будь-яких цілих невід’ємних чисел а і b справджується рівність а×b=b×а. Теорема 8 (сполучний або асоціативний закон множення): для будь-яких цілих невід’ємних чисел а, b і с справджується рівність (а×b)×с=а×(b×с). Доведення теорем 7 і 8 проводиться аналогічно до доведення теореми 9, а тому пропонуємо провести їх самостійно. Для доведення теорем 7 і 8 виконайте завдання № 3 для самостійної роботи.Наступна теорема 9 пов’язує операції додавання і множення. Теорема 9 (лівий та правий дистрибутивні або розподільні закони множення відносно додавання): для будь-яких цілих невід’ємних чисел а, b і с справджуються рівності: 1) с×(а+b)=с×а+с×b; 2) (а+b)×с=а×с+b×с. Доведення: Для доведення рівності 2 використаємо означення добутку через суму однакових доданків: (а+b)×с=(а+b)+(а+b)+(а+b)+...(а+b)=(а+а+а+...+а)+(b+b+b+...+b)=ас+bс
С с с Отже, (а+b)×с=а×с+b×с. Рівність (1) пропонуємо довести самостійно. Теорему доведено. Прийняті нами означення суми і різниці можна поширити на множину цілих невід’ємних чисел, де Z0=N0=NÈ{0}. Оскільки 1) АÈÆ=ÆÈА=А, то а+0=0+а=а; 2) А\Æ=А, а тому а-0=а.
Визначення частки цілого невід’ємного числа на натуральне число через розбиття множини на класи, що попарно не перетинаються. Ділення на множині цілих невід’ємних чисел, зв'язок ділення з множенням. Теореми про існування та єдиність частки. 9. На практиці досить часто доводиться розв'язувати задачі таких двох видів: 1) дано скінченну множину А і її слід розбити на певне число еквівалентних між собою підмножин без спільних елементів, а потім визначити потужність кожної із цих підмножин. Такі задачі називають задачами на ділення на рівні частини; 2) дано власну підмножину В скінченної множини А і необхідно визначити скільки всіх підмножин без спільних елементів, еквівалентних множині В, має множина А. Такі задачі називають задачами на ділення на вміщення. Таким чином, в обох випадках множина А повинна бути представлена у вигляді об'єднання скінченної кількості еквівалентних між собою множин:А=В1ÈВ2ÈВ3È...ÈВk, причому В1~В2~В3~...~Вk. При розв'язування першої задачі (задачі на ділення на рівні частини) завдання полягає в тому, щоб визначити потужність кожної із еквівалентних підмножин. Розв'язування другої задачі (задачі на ділення на вміщення) зводиться до відшукання кількості таких еквівалентних між собою підмножин. Якщо перейти до характеристики потужності множини А і вказаних підмножин, тобто позначити n(А)=а, n(В1)=n(В2)=n(В3)=...=n(Вk)=x, то ми приходимо до поняття нової арифметичної операції на множині цілих невід’ємних чисел, а саме до операції ділення на натуральне число. У першому випадку число а=n(А) слід представити у вигляді суми відомого числа b однакових доданків, кількість яких (х) необхідно знайти. При розв'язуванні другої задачі число а слід представити у вигляді суми невідомого числа (х) однакових доданків, кожен з яких дорівнює b. Символічно це можна записати в таблиці (див. таблицю № 3.1.).
Таблиця № 3.1.
Отже, розв'язування задачі на ділення на рівні частини зводиться до відшукання за відомим добутком і відомим другим множником невідомого першого множника, а задачі на ділення на вміщення – до відшукання за відомим добутком і відомим першим множником невідомого другого множника (див. таблицю № 3.1.). Обидві задачі розв'язуються дією, оберненою до дії множення, а саме: х=а:b. Тепер можна ввести такі означення. Означення 1: часткою натуральних чисел а і b називається число елементів кожної із еквівалентних підмножин, на які розбито множину А, де а=n(А) і b – число підмножин, на які розбито множину А. Означення 2: часткою натуральних чисел а і b називається число еквівалентних підмножин, на які розбито множину А, де а=n(А) і b=n(В1)=n(В2)=n(В3)=...=n(Вх). Визначаючи частку натуральних чисел, ми використовували операцію розбиття множини на підмножини, які попарно не перетинаються. Разом з тим, ми показали, що в обох випадках приходимо до дії, оберненої до дії множення. Отже, можна ввести таке означення. Означення 3: часткою від ділення натуральних чисел а і b називається таке третє натуральне число а:b, яке в добутку з числом b дає нам число а, тобто b×(а:b)=а. Число а називають діленим, число b – дільником, а число а:b – часткою. Операція, за допомогою якої знаходиться частка, називається операцією ділення на множині натуральних чисел. Зазначимо, що всі прийняті нами означення рівносильні між собою, але в жодному із них не говориться про існування та єдиність операції ділення. Саме тому, розглянемо це питання. Дія ділення зводиться до розв'язування лінійного рівняння bх=а. Із курсу математики середньої школи відомо, що це рівняння: 1) при а=b=0 набуває вигляду 0×х=0 і має нескінченну множину розв’язків. Отже, вираз 0:0 не має жодного конкретного значення, тобто не має смислу. Саме тому, ділити на нуль не можна!; 2) при а=0 і b¹0 рівняння набуває вигляду b×х=0 і має єдиний розв’язок х=0; 3) при а¹0 і b¹0 рівняння bх=а матиме розв’язок на множині натуральних чисел тоді, коли а ділиться націло на b. Для відповіді на запитання про існування частки слід довести наступну теорему. Теорема 10 (про існування частки): частка цілого невід’ємного числа а на натуральне число b існує тоді і тільки тоді, коли а ділиться націло на b. Доведення: Доведення теореми буде складатися із двох частин: у першій слід довести достатню умову, а у другій – необхідну умову існування частки. Доведемо достатню умову, яка формулюється так: “якщо ціле невід’ємне число а ділиться націло на натуральне число b, то частка а:b існує”. За умовою а ділиться націло на b. Це означає: існує таке число с, що b×с=а. Отже, с=а:b. Достатню умову доведено. Доведемо необхідну умову, яка формулюється так: “якщо частка а:b існує, то число а ділиться націло на b”. За умовою частка а:b існує. Це означає, що b×(а:b)=а, тобто число а ділиться націло на число b. Необхідну умову доведено. Таким чином, теорему доведено повністю. Теорема 11 (про єдиність частки): якщо частка від ділення цілого невід’ємного числа а на натуральне число b існує, то вона єдина. Доведення: Доведення цієї теореми проведемо методом від супротивного так, як ми це робили при доведенні єдиності різниці. Припустимо, що частка не єдина, тобто існує принаймні дві частки. Нехай а:b=с1 і а:b=с2, причому с1¹с2. Згідно означення частки маємо а=bс1 і а=bс2. Звідси bс1=bс2. Отже, с1=с2, а це суперечить вибору чисел с1 і с2. Ця суперечність дозволяє стверджувати, що наше припущення про не єдиність частки було хибним. Таким чином, якщо частка існує, то вона єдина. Теорему доведено.
Поиск по сайту: |
 Для доведення теореми використаємо означення добутку через суму однакових доданків, розглянувши три випадки: 1) b=0; 2) b=1; 3) b>1. Якщо b=0, то добуток а×0 існує згідно з додатковим означенням: а×0=0. Якщо b=1, то добуток а×1 також існує згідно з додатковим означенням: а×1=а. В обох випадках добутки єдині. Якщо b>1, то добуток існує і єдиний, бо існує і єдина сума а+а+а+...+а=а×b. Теорему доведено.
Для доведення теореми використаємо означення добутку через суму однакових доданків, розглянувши три випадки: 1) b=0; 2) b=1; 3) b>1. Якщо b=0, то добуток а×0 існує згідно з додатковим означенням: а×0=0. Якщо b=1, то добуток а×1 також існує згідно з додатковим означенням: а×1=а. В обох випадках добутки єдині. Якщо b>1, то добуток існує і єдиний, бо існує і єдина сума а+а+а+...+а=а×b. Теорему доведено.
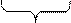 а=х+х+х+...+х=х×b
b
а=х+х+х+...+х=х×b
b
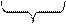 а=b+b+b+...+b=b×х
х
а=b+b+b+...+b=b×х
х