Операція еквіваленції предикатів.

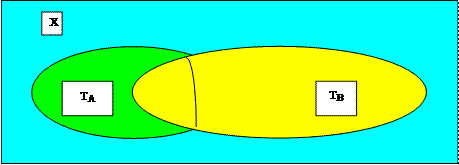
7.2. Для того, щоб визначити операцію еквіваленції предикатів, розглянемо на множині абітурієнтів два предикати: А(х): „х – склав всі екзамени” і В(х): „х – набрав прохідний бал”. Як можна назвати предикат „для того, щоб х – склав всі екзамени, необхідно і достатньо, щоб він набрав прохідний бал” – еквіваленцією заданих предикатів. Отже, приймемо таке означення.

Означення: еквіваленцією двох предикатів А(х) і В(х), заданих на одній і тій самій множині Х, називається такий новий предикат А(х)↔В(х), який визначений на тій самій множині Х і який істинний при всіх тих хÎХ, при яких значення істинності предикатів А(х) і В(х) співпадають.

Оскільки при оперуванні із складенимипредикатами доводиться знаходити їх множини істинності, то знайдемо множину істинності предиката А(х)↔В(х). Позначимо область визначення предикатів через Х, множину істинності предиката А(х) через Т_А, а множину істинності предиката В(х) – через Т_В. Щоб знайти множину істинності предиката А(х)↔В(х), тобто Т_А↔_В, можна використати міркування або діаграми Ейлера-Венна. Зазначимо, що міркуваннями множину істинності Т_А↔_В можна знайти, використавши рівність А(х)↔В(х)=((Ā(х)ÚВ(х))Ù(В(х)ÚА(х))). Отже, маємо: Т_А↔_В=(Т_АÈТ_В)Ç(Т_ВÈТ_А).Оскільки відомо, що предикат А(х)↔В(х) буде істинним для тих значень хєХ, для яких предикати А(х) і В(х) одночасно істинні або хибні, тобто на множинах Т_АÇТ_В і Т_{`А</sub>ÇТ<sub>`в}. Отже, множиною істинності предиката А(х)↔В(х) – є об'єднання цих множин, тобто Т_А↔_В=(Т_АÇТ_В)È(Т_{`А</sub>ÇТ<sub>`в}) (див. діаграму № 2.7.).

Діаграма № 2.7. Множина істинності еквіваленції предикатів.

Логічні формули. Порядок виконання логічних операцій у формулах. Рівносильні формули. Тотожньо істинні формули (логічні закони). Відношення логічного слідування та рівносильності на множині предикатів.

8. Із шкільного курсу математики відомо, що вирази отримують за допомогою цифр, букв, знаків арифметичних дій та дужок. Аналогічно можна отримувати вирази або формули у математичній логіці. Для того, щоб однозначно розуміти відповідні формули та в однаковому порядку виконувати дії над висловленнями та предикатами, виробили наступні правила виконання операцій: заперечення, кон’юнкція, диз’юнкція, імплікація та еквіваленція:

1) порядок виконання логічних операцій регулюють дужками, починаючи виконання з операції, яка стоїть у самих внутрішніх дужках;

2) вираз, якій міститься під знаком операції заперечення, в дужки не береться, але його вважають таким, що знаходиться в дужках, а тому обчислюють окремо;

3) якщо у формулі немає дужок, то порядок виконання логічних операцій такий: а) заперечення; б) кон’юнкція; в) диз’юнкція; г) імплікація; д) еквіваленція. Застосування вказаних правил проілюструємо на наступній вправі.

Вправа: спростити вираз (aÚbÚcÚd)Ù(aÚbÚcÚd)Ù(aÚbÚc)Ù(aÚb)Ùā=(aÚbÚc)Ù(dÚd)Ù(aÚbÚc)Ù(aÚb)Ùā=(aÚbÚc)Ù1Ù(aÚbÚc)Ù(aÚb)Ùā=(aÚbÚc)Ù(aÚbÚc)Ù(aÚb)Ùā=(aÚb)Ù(сÚс)Ù(aÚb)Ùā=(aÚb)Ù1Ù(aÚb)Ùā=(aÚb)Ù(aÚb)Ùā=aÙ(bÚ b)Ùā=aÙ1Ùā=aÙā=0.

Побудуємо таблицю істинності для двох формул: a↔b і a→b.

Аналіз таблиці № 2.11. дозволяє зробити висновок про те, що формула a→b набуває значення 1 при тих значеннях логічних змінних, при яких формула a↔b також набуває значення 1. В цьому випадку говорять, що формула a→b логічно випливає з формули a↔b. Символічно це позначають так a↔b╞a→b, а читають цей запис наступним чином: формула a→b логічно випливає з формули a↔b.

Таблиця № 2.11.

Означення: формула b називається логічним наслідком формули а (або формула b логічно випливає з формули а), якщо формула b набуває значення 1 при всіх тих наборах значень логічних змінних, при яких формула а також набуває значення 1.

Нехай на множині Х задано предикати А(х) і В(х) такі, що їх множини істинності Т_А і Т_В знаходяться у відношенні Т_АÌТ_В. З’ясуємо, якою буде імплікація А(х)→В(х) при певних значеннях хєХ. Виберемо довільне аєХ. При цьому можливі два випадки: 1) аєТ_А. Тоді аєТ_В, а тому А(а)=1 і В(а)=1, тобто А(а)→В(а)=1→1=1; 2) аєТ_А. Тоді А(а)=0, а імплікація А(а)→В(а)=0→В(а)=1. В таких випадках також говорять, предикат В(х) логічно випливає або логічно слідує із предиката А(х). Символічно це позначають так: А(х)╞ В(х).

Означення: якщо предикати А(х) і В(х) задані на одній множині Х, то кажуть, що предикат А(х) логічно випливає із предиката В(х), тоді і тільки тоді, коли Т_АÌТ_В.

Означення: якщо імплікація А(х)→В(х)=1 при всіх хєХ, то говорять, що предикат В(х) логічно слідує з предиката А(х).

Про такі предикати говорять, що вони знаходяться у відношення логічного слідування. Як же визначити чи знаходяться предикати у відношенні логічного слідкування? – слід дотримуватися такого алгоритму: 1) з’ясувати, чи на одній множині задані обидва предикати; 2) знайти множини істинності кожного з предикатів; 3) виявити співвідношення між множинами істинності предикатів; 4) якщо одна з множин істинності є підмножиною іншої, то зробити висновок про відношення логічного слідування між предикатами. Проілюструємо сказане на наступному прикладі.

Вправа: з’ясувати, чи знаходяться предикати А(х): «натуральне число х ділиться на 4» і В(х): «натуральне число х- парне» у відношенні логічного слідування.

Розв’язування:

В обох предикатах мова йде про натуральні числа, а тому областю визначення предикатів є множина натуральних чисел. Отже, предикати задані на одній множині. Знайдемо множини істинності предикатів. Т_А={4, 8, 12, 16, …, 4n, …}. Т_В={2, 4, 6, 8, …, 2n, …}. Звідси легко бачити, що Т_АÌТ_В. Таким чином, А(х)╞ В(х). Предикат А(х)→В(х) можна прочитати так: із того, що натуральне число ділиться націло на 4, логічно слідує, що натуральне число парне. До розв’язування цієї вправи можна підійти по-іншому. Утворимо імплікацію заданих предикатів А(х)→В(х). Легко бачити, що вона істинна. Отже, відповідно до другого означення можна твердити, що А(х)╞ В(х).

Розглядаючи предикати, ми не цікавилися питанням про те, яке співвідношення може існувати між областю визначення предиката і множиною його істинності. Виявляється, що при співпаданні цих множин приходимо до поняття рівносильності предикатів.

Означення: два предикати А(х) і В(х), які задані на множині Х, називаються рівносильними, якщо еквіваленція цих предикатів А(х)↔В(х) істинна при всіх хєХ (тобто, коли Х=Т_А↔_В).

Символічно це записують так: А(х)≡В(х). Щоб перевірити, чи рівносильні предикати слід з’ясувати наступне: 1) чи задані предикати на одній множині; 2) утворити еквіваленцію заданих простих предикатів; 3) знайти множину істинності еквіваленції; 4) порівняти область визначення та множину істинності; 5) якщо вони співпадають, то зробити висновок про те, що предикати знаходяться у відношенні рівносильності.

Вправа: з’ясувати, чи рівносильні предикати А(х): «натуральне число х ділиться націло на 5» і В(х): «десятковий запис натурального числа х закінчується на 0 чи 5».

Розв’язання:

Легко бачити, що предикати задані на одній множині натуральних чисел. Утворимо еквіваленцію А(х)↔В(х): «натуральне число х ділиться націло на 5 тоді і тільки тоді, коли його десятковий запис закінчується цифрами 0 чи 5». Отже, А(х)↔В(х)=1 при всіх хєХ, а тоді Т_А↔_В=Х. Таким чином, А(х)≡В(х).

Розглянемо деяку імплікацію А(х)→В(х), де хєХ. Нехай вона істинна при всіх хєХ. Якщо такі умови виконуються, то предикат А(х) називають достатньою умовою для предиката В(х), а предикат В(х) – необхідною умовою для предиката А(х). Якщо одночасно А(х)→В(х)=1 і В(х)→А(х)=1 при всіх хєХ, то кожен із предикатів називають необхідною і достатньою умовою для іншого. Теореми, які сформульовані у термінах необхідно і достатньо, називають ознаками. Прикладом ознак є ознаки подільності чисел, ознаки паралелограма, паралельності прямих і площин тощо.

Логічні операції над висловленнями (Ù, Ú, →, ↔, ¾) до певної міри відповідали сполучникам, словосполученням, частці „не”. Квантор існування можна розглядати як узагальнення диз'юнкції. Дійсно, нехай Х={а₁, а₂, а₃,...а_к} Р(х), де хÎХ, тоді висловлення... ($х)Р(х) рівносильне диз'юнкції Р(а₁)ÚР(а₂)Ú...ÚР(а_к). Квантор загальності можна розглядати, як узагальнення операції кон'юнкції. Дійсно, якщо Р(х), де хÎХ={а₁, а₂, а₃,..., а_к}, то висловлення ("х)Р(х) рівносильне кон'юнкції Р(а₁)Ù Р(а₂)Ù... Ù Р(а_к). Не важко здогадатися, що операції об’єднання в алгебрі множин відповідає операція диз’юнкції із алгебри висловлень, операції перетину – операція кон’юнкції, операції доповнення – операція заперечення. Ми з Вами розглянули основні операції алгебри висловлень та їх основні властивості (аÚв=вÚа, аÙв=вÙа, аÚ(вÚс)=(аÚв)Úс, аÙ(вÙс)=(аÙв)Ùс, аÙ(вÚс)=(аÙв)Ú(аÙс), аÚ(вÙс)=(аÚв)Ù(аÚс), аÚ0=0Úа=а, аÙ0=0Ùа=0, аÚ1=1Úа=1, аÙ1=1Ùа=а, аÙа=а, аÚа=а тощо). Побудувавши таблиці істинності можна довести справедливість наступних законів:

1. аÚ`а=1 – закон виключеного третього.

2. а Ù`а = 0 – закони несуперечливості

­­­­­­­­­­­­ а Ù `а = 1

Запитання для самоконтролю та самостійної роботи студентів за змістовним модулем 2.2.

1. Запишіть довільне висловлення та утворіть його заперечення двома способами.

2. Довести справедливість закону подвійного заперечення висловлень, побудувавши таблицю істинності.

3. Довести справедливість закону подвійного заперечення предикатів, побудувавши таблицю істинності.

4. Довести, побудувавши таблицю істинності, комутативний закон операції кон’юнкції, а саме: аÙв=вÙа.

5. Записати закони операції кон’юнкції предикатів, використавши закони операції кон’юнкції висловлень.

6. Самостійно довести, побудувавши таблиці істинності, комунікативний, асоціативний, два дистрибутивні та перший закон де Моргана.

7. Записати самостійно закони, яким підкоряється операція диз’юнкції предикатів.

8. Пропонуємо студентам довести обидві формули (1) а↔b=(а→b)Ù(b→а); 2) а↔b=(āÚb)Ù(bÚа)), побудувавши таблиці істинності (див. завдання для самостійної роботи).

9. Довести самостійно, побудувавши таблицю істинності, закон виключеного третього та закони несуперечливості.

Поиск по сайту: