 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Примеры решения типовых задач. 3.1.Плоская электромагнитная волна с частотой 109 Гц распространяется в среде с
3.1.Плоская электромагнитная волна с частотой 109 Гц распространяется в среде с параметрами Определить фазовую скорость, длину волны и коэффициент ослабления. Решение. Учтем, что
Таким образом, для диэлектриков с малыми потерями коэффициент фазы и коэффициент ослабления приближенно равны:
Используя соотношение (4.4), найдем фазовую скорость волны
Полученный результат показывает, что наличие потерь в среде приводит к изменению величины фазовой скорости. Для
По известной величине фазовой скорости найдем длину волны:
Подстановка исходных данных в полученную ранее формулу дает:
3.2.Вычислить фазовую скорость, коэффициент ослабления и глубину проникновения поля для плоской электромагнитной волны c частотой 10МГц, распространяющейся в металле с параметрами σ =5·107 См/м, µ = 1. Решение. В реальных металлах плотность токов проводимости значительно больше плотности токов смещения. Поэтому выражение (3.3) можно приближенно представить в виде
Коэффициент фазы и коэффициент ослабления в рассматриваемой среде численно равны друг другу:
По известной величине β можно вычислить фазовую скорость:
Под глубиной проникновения поля в металл и понимают расстояние, на котором его амплитуда уменьшается в е раз. Очевидно, что
3.3.Плоская электромагнитная волна с частотой 109 Гц распространяется в среде с параметрами ε = 2,25, tgδэ = 0,01, µ = 1. Амплитуда электрического поля в плоскости z = 0 равна 100 В/м. Определить среднюю плотность потока мощности в плоскости z =1 м. Решение. Плотность потока мощности плоской электромагнитной волны определяется выражением
Таким образом, необходимо вычислить коэффициент ослабления и характеристическое сопротивление. Действуя так же, как в задаче 4.1, можно найти α. Подстановка исходных данных дает α = 0,162 м-1. При определении характеристического сопротивления для tgδэ<< 1 можно использовать приближенное выражение для квадратного корня, входящего в формулу (3.10). Тогда
Следовательно,
или после необходимых вычислений Пср(z = 1) = 14,38 Вт/м2. 3.4.Доказать, что в средах без потерь фазовый фронт и плоскость равных амплитуд неоднородных плоских волн образуют между собой угол 90°. Решение. В средах без потерь коэффициент распространения γ – действительная величина. Поэтому, если
а уравнением для плоскости равных амплитуд будет
Косинус угла между двумя плоскостями
С помощью выражения (4.11) можно найти, что
и, следовательно, угол ψ действительно равен 90°. 3.5.Вывести формулу для определения коэффициента эллиптичности (отношение большой оси эллипса к малой) плоской электромагнитной волны, для которой в плоскости z = 0 поля имеют вид
Найти ориентацию осей эллипса по отношению к осям системы координат. Решение. Перейдем от комплексных амплитуд к мгновенным значениям и введем новые переменные ξ и η:
Разложим косинусы суммы аргументов и решим эти два уравнения относительно соsωt и sinωt:
Возводя эти уравнения в квадрат и исключив переменную t, получим
где
В системе координат (ξ, η) это есть уравнение эллипса. Путем поворота осей на угол α, удовлетворяющий условию
преобразуем уравнение к каноническому виду
Используя [3], найдем полуоси эллипса
Теперь можно вычислить коэффициент эллиптичности как отношение а к b. В результате несложных преобразований получим
Ориентация осей эллипса по отношению к оси х исходной системы координат определяется углом α, отсчитываемым против часовой стрелки, если смотреть с конца вектора 1z. 3.6.Некоторые вещества (например, водный раствор сахара) имеют различную скорость распространения для волн с левой и правой круговой поляризацией. Это приводит к повороту плоскости поляризации плоской волны с линейной поляризацией в процессе ее распространения. Такое свойство веществ называют оптической активностью. Считая заданными значения фазовых скоростей для левой υл и правой υп круговой поляризации, вывести формулу, определяющую угол поворота плоскости поляризации волны на участке пути длиной h для электромагнитной волны с заданной частотой ω. Решение. Линейно поляризованную волну, имеющую в плоскости z = 0 вид
можно представить как сумму двух волн с круговой поляризацией:
Волна с правой круговой поляризацией при распространении в направлении оси z будет описываться выражением
а с левой – выражением
В любой плоскости z ≠0 сумма этих волн будет представлять собой волну с линейной поляризацией. Координатные составляющие этой волны равны:
Суммарный вектор Е образует некоторый угол j с осью х координатной системы (х, у, z), который зависит от z. Тангенс этого угла
Таким образом, угол поворота плоскости поляризации на отрезке пути длиной L определяется из формулы
Обычно различие скоростей распространения υл и υпмало. Поэтому приближенно
где υ – среднее значение скорости; δυ– относительная разность скоростей распространения; λ =υ / f – длина волны в среде.
Поиск по сайту: |
 .
. и разложим выражение (4.3) в степенной ряд. Ограничиваясь тремя первыми членами, получим
и разложим выражение (4.3) в степенной ряд. Ограничиваясь тремя первыми членами, получим .
. ,
, .
.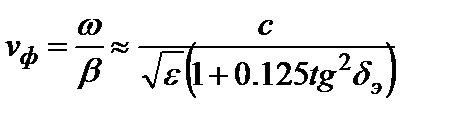 .
. поправка составляет 0,125%, так что практически можно положить
поправка составляет 0,125%, так что практически можно положить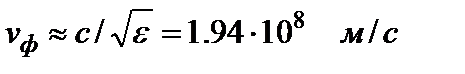
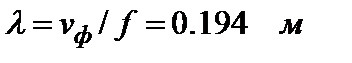 .
. .
. .
. .
. .
.
 .
. .
.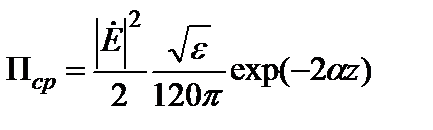 ,
, то уравнение для фазового фронта имеет вид
то уравнение для фазового фронта имеет вид ,
, ,
, .
. ,
,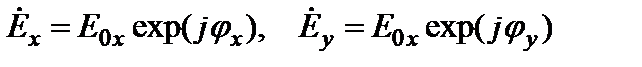 .
.
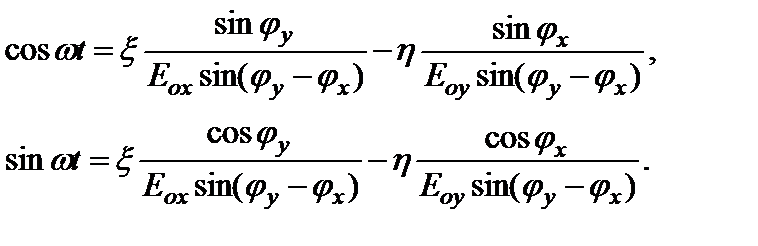
 ,
,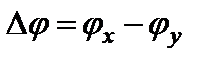 .
. ,
, .
.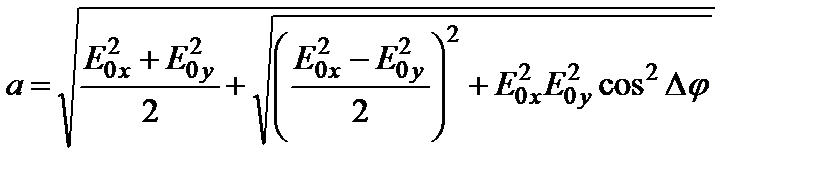 ,
, ..
..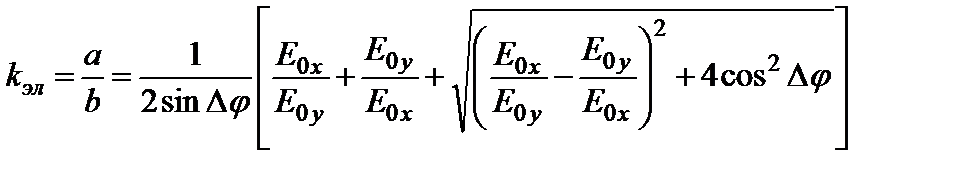 .
. ,
, .
. ,
, .
.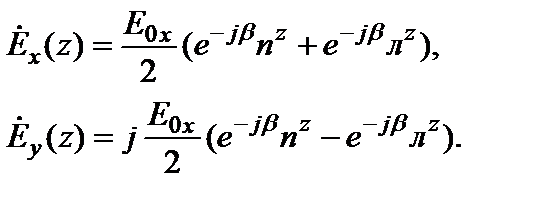
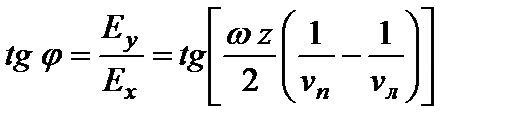 .
.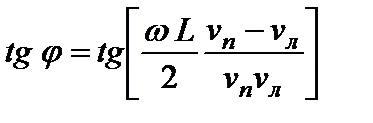 .
. ,
,