 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Примеры решения типовых задач. 2.1.В вакууме существует электромагнитное поле, гармонически изменяющееся во времени
2.1.В вакууме существует электромагнитное поле, гармонически изменяющееся во времени. В некоторой точке пространства вектор Определить плотность тока смещения в данной точке. Решение. По определению ток смещения
Следует обратить внимание на то, что в пространстве ток смещения и напряженность электрического поля параллельны, однако ток опережает по фазе напряженность поля на 90°. 2.2.Показать, что из уравнений Максвелла для вакуума следуют известные волновые уравнения
Решение. Выпишем систему из двух первых уравнений Максвелла, справедливых для вакуума в отсутствие сторонних источников:
и применим операцию rot ко второму уравнению системы (2.27):
Предполагая, что в интересующей нас области пространства нет зарядов (divЕ = 0) и воспользовавшись первым уравнением (2.27), получим волновое уравнение (2.26) для вектора электрического поля. Уравнение относительно вектора магнитного поля находят аналогично. 2.3.Материальная среда характеризуется абсолютными проницаемостями: Вывести дифференциальное уравнение второго порядка, которому должно удовлетворять векторное поле Н в данной неоднородной среде, если электромагнитный процесс гармонически изменяется во времени с частотой ω. Решение. Рассмотрим два первых уравнения Максвелла относительно комплексных амплитуд:
и применим операцию rot к первому уравнению (2.28):
Магнитная проницаемость среды неизменна в пространстве, поэтому
Вектор Е можно выразить через вектор Н из первого уравнения (2.28):
Отсюда получаем окончательный вид искомого уравнения
2.4.Показать, что уравнение непрерывности тока вытекает из первого и третьего уравнений Максвелла (2.1). Решение. Здесь следует принять во внимание известное тождество векторного анализа и записать
а затем воспользоваться третьим уравнением Максвелла (2.1). Таким образом, приходим к уравнению непрерывности
2.5.Нестационарные задачи теории электромагнитного поля удобно решать операторным мето дом подобно тому, как это делается при изучении переходных процессов в линейных электрических цепях. Вводя изображения векторов поля:
Найти операторную форму уравнений Максвелла для вакуума в отсутствие сторонних источников. Решение. Преобразуем по Лапласу обе части системы уравнений Максвелла (2.27). Векторные дифференциальные операции проводят по пространственным координатам, поэтому оператор rot может быть вынесен за знак интеграла. Если полю Е соответствует изображение ℜ, то изображением производной ∂Е/∂t будет выражение рℜ - Е(r, 0), которое учитывает начальное состояние поля при t=0. Таким образом, получается система уравнений Максвелла относительно изображений:
2.6.Имеется плоская граница раздела двух сред, обладающих относительными диэлектрическими проницаемостями ε1 и ε2 (рис. 2.1). Силовые линии электрического поля в первой среде образуют угол ϑ1 с направлением нормали. Найти ориентацию силовых линий поля во второй среде. Рис. 2.1. Решение: Воспользуемся граничными условиями
или Деля эти уравнения друг на друга, получим
Отметим, что если ε2 →∞, то 2.7.В некоторой точке пространства заданы комплексные амплитуды векторов поля:
Найти мгновенные значения векторов поля, а также среднее значение вектора Пойнтинга. Решение. Мгновенные значения связаны c комплексными амплитудами известными формулами
откуда
Для полей, гармонически изменяющихся во времени,
Поиск по сайту: |
 .
. ,
, . (2.26)
. (2.26)
 (2.27)
(2.27)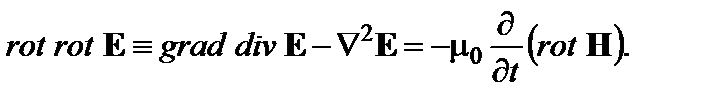
 ,
,  .
. ,
, . (2.28)
. (2.28)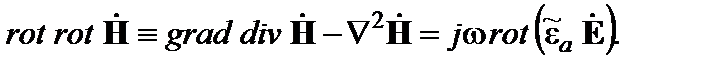
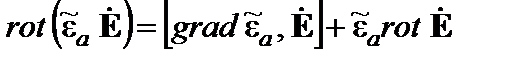 .
.
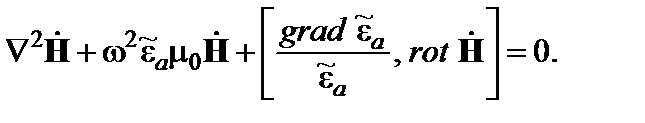
 ,
, .
. ,
, .
.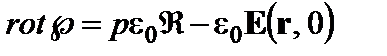 ,
, .
. ,
,  ,
, ,
, 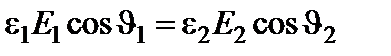 .
. , или
, или  .
. → π/2 независимо от ориентации поля в первой среде.
→ π/2 независимо от ориентации поля в первой среде. ,
, .
.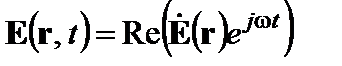 ,
, ,
,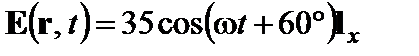 ,
, .
. (Вт/м2).
(Вт/м2).