 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоретические сведения. Плоские электромагнитные волны существуют в однородных безграничных средах
Плоские электромагнитные волны существуют в однородных безграничных средах. В случае полей, изменяющихся во времени по гармоническому закону, комплексные амплитуды Е и Н удовлетворяют уравнениям Гельмгольца
где Так как исходные уравнения Максвелла дают однозначную связь между Е и Н, достаточно найти решение лишь одного из этих уравнений. Частное решение уравнения Гельмгольца описывает однородную плоскую волну. Если последняя распространяется вдоль оси z декартовой системы координат, то указанное решение имеет вид:
Первое слагаемое соответствует прямой (падающей) волне, распространяющейся в направлении положительных значений z, второе слагаемое - обратной (отраженной) волне, распространяющейся в направлении отрицательных значений. Если величины
где На высоких частотах магнитные свойства большинства сред выражены слабо. Поэтому с достаточной для практических целей степенью точности можно считать
Поскольку
комплексный коэффициент распространения
Коэффициент фазы β характеризует изменение фазы гармонических колебаний при распространении волны. Расстояние, на котором фаза изменяется на 2π рад, называется длиной волны:
Плоскость равных фаз называется фазовым фронтом волны, а скорость перемещения этой плоскости – фазовой скоростью:
Коэффициент фазы и коэффициент ослабления могут быть выражены следующими формулами:
Таким образом, между ними существует соотношение
Фазовая скорость
длина волны
Отношение фазовой скорости в среде к скорости света называют коэффициентом преломления:
Из уравнений Максвелла следует, что в случае плоской волны комплексные амплитуды векторов Е и Н связаны характеристическим сопротивлением среды:
так что
Характеристическое сопротивление для немагнитных сред
Аргумент принимает значения от нуля (диэлектрики без потерь) до π/4 (идеальный металл). Характеристическое сопротивление для вакуума
Векторные уравнения (4.1) означают, что любая координатная составляющая векторов поля удовлетворяет уравнению
имеющему в декартовой системе координат частное решение
Здесь С – константа;
Если – вещественные числа, то выражение (3.10) описывает однородную плоскую волну, распространяющуюся в произвольном относительно исходной системы координат направлении. Эту волну удобно выразить формулой
Числа
у которой фазовый фронт задается уравнением
а плоскость равных амплитуд – уравнением
В общем случае фазовый фронт и плоскость равных амплитуд образуют между собой произвольный угол. Поскольку уравнения Максвелла линейны, любая комбинация их решений также является решением. В частности, если
также есть решение уравнений Максвелла и, следовательно, оно описывает распространение в пространстве некоторой волны. В зависимости от соотношения между фазами и амплитудами Линейно поляризованная волна представляет собой один из предельных случаев эллиптически поляризованной волны. Второй предельный случай имеет место при равенстве амплитуд исходных полей и сдвиге фаз между ними, равном 90°. Здесь конец вектора Е перемещается по окружности, и волна называется волной с круговой поляризацией. Поле такой волны можно представить выражением
Знак минус соответствует волне с правой круговой поляризацией, у которой вектор Е вращается по часовой стрелке (если смотреть в направлении распространения), а знак плюс – волне с левой круговой поляризацией (направление вращения обратное). Любая волна с линейной поляризацией может быть представлена суммой двух волн с круговой поляризацией, например
где
Плоская волна переносит энергию в направлении распространения. Для гармонических полей этот процесс описывается средним значением вектора Пойнтинга:
ЧастоПср удобно выражать только через напряженность электрического или магнитного поля:
В средах без потерь Пср не зависит от координаты z. Если же среда обладает потерями, то плотность потока мощности плоской электромагнитной волны убывает при распространении по экспоненциальному закону:
Величину потерь в среде характеризуют погонным затуханием ∆ в дБ/м:
связанным с коэффициентом ослабления к соотношением ∆ = 8,69α. Фазовая скорость плоской электромагнитной волны в среде с зависящими от частоты параметрами ε' и ε'' также является функцией частоты. Такое явление называют дисперсией фазовой скорости. При распространении сложных сигналов в этом случае будут нарушаться исходные амплитудные и фазовые соотношения между отдельными составляющими спектра и, как следствие, будет изменяться форма сигнала в процессе его распространения. Для нахождения вида сигнала необходимо пользоваться спектральным или операторным методом, Например, полагая, что
есть Фурье-преобразование сигнала в плоскости z = 0, можно найти сигнал для любых значений z, используя обратное преобразование
Пренебрегая потерями в среде и полагая, что сигналы s(t,z) являются узкополосными, можно показать, что их огибающая в средах с дисперсией распространяется с групповой скоростью
Если условие узкополосности сигнала не выполняется, то понятие групповой скорости, строго говоря, перестает адекватно описывать трансформацию формы такого сигнала.
Поиск по сайту: |
 ,
, (3.1)
(3.1) – комплексный коэффициент распространения, β – коэффициент фазы, или волновое число; α – коэффициент ослабления.
– комплексный коэффициент распространения, β – коэффициент фазы, или волновое число; α – коэффициент ослабления. (3.2)
(3.2) и
и  известны, то β и α можно найти с помощью выражения для корня квадратного из комплексного числа:
известны, то β и α можно найти с помощью выражения для корня квадратного из комплексного числа: ,
, – модуль комплексного числа; квадратные корни
– модуль комплексного числа; квадратные корни 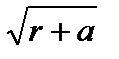 и
и  следует считать положительными.
следует считать положительными.
 ,
, . (3.3)
. (3.3) .
.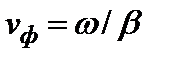 . (3.4)
. (3.4)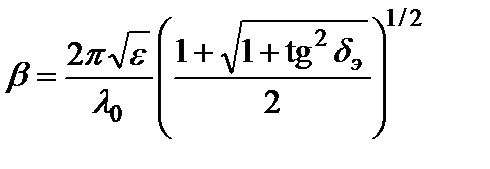 , (3.5)
, (3.5) . (3.6)
. (3.6)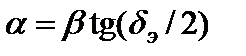 .
.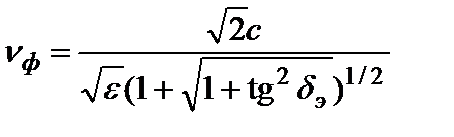 , (3.7)
, (3.7) . (3.8)
. (3.8)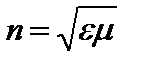 .
. , (3.9)
, (3.9) .
.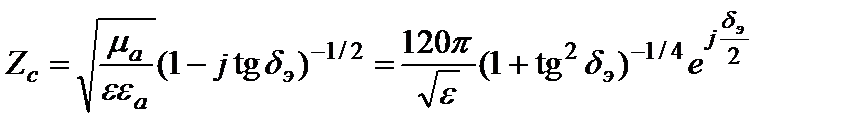 Ом.
Ом.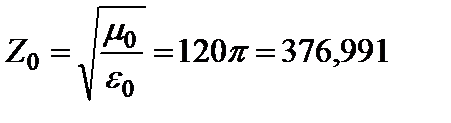 Ом.
Ом.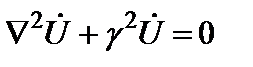 ,
, . (3.10)
. (3.10) – комплексные постоянные, удовлетворяющие условию
– комплексные постоянные, удовлетворяющие условию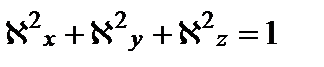 (3.11)
(3.11) . (3.12)
. (3.12)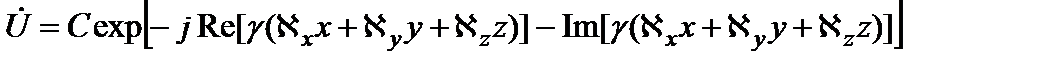 , (3.13)
, (3.13) ,
,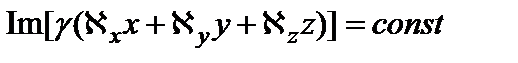 .
. и
и  – решения исходных уравнений, то
– решения исходных уравнений, то . (3.14)
. (3.14) и
и 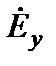 в каждой точке пространства конец вектора Е будет перемещаться по эллипсу с различным отношением и ориентацией его полуосей. Такая волна называется волной с эллиптической поляризацией. При произвольном значении амплитуд и фаз в выражении (3.14) путем поворота осей вокруг оси z всегда можно ввести новую систему координат (х', у', z'), в которой сдвиг фаз между координатными составляющими будет равен ±90°, а полуоси эллипса – совпадать с направлением осей системы. Угол поворота, обеспечивающий такое преобразование системы координат, будет определять ориентацию осей эллипса в системе (х, у, z). Отношение большой полуоси эллипса к малой называют коэффициентом эллиптичности kэл.
в каждой точке пространства конец вектора Е будет перемещаться по эллипсу с различным отношением и ориентацией его полуосей. Такая волна называется волной с эллиптической поляризацией. При произвольном значении амплитуд и фаз в выражении (3.14) путем поворота осей вокруг оси z всегда можно ввести новую систему координат (х', у', z'), в которой сдвиг фаз между координатными составляющими будет равен ±90°, а полуоси эллипса – совпадать с направлением осей системы. Угол поворота, обеспечивающий такое преобразование системы координат, будет определять ориентацию осей эллипса в системе (х, у, z). Отношение большой полуоси эллипса к малой называют коэффициентом эллиптичности kэл. (3.15)
(3.15) , (3.16)
, (3.16) (3.17)
(3.17) . (3.18)
. (3.18) (3.19)
(3.19) . (3.20)
. (3.20) ,
,
 . (3.21)
. (3.21)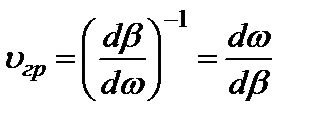 . (3.22)
. (3.22)