 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Элементы векторного анализаСтр 1 из 7Следующая ⇒
Семинар №1. § 1.1. Основные теоретические сведения. Для описания физических полей принято использовать их математические модели - скалярные и векторные поля. В произвольной системе координат
Для характеристики величины и направления скорости изменения скалярного поля в пространстве вводят градиент этого поля
где Приведем значения коэффициентов Лямэ для наиболее употребительных координатных систем: декартова система координат (х, у, z)
цилиндрическая система координат (r, φ, z)
сферическая система координат (r, θ, φ)
Конкретно градиент вычисляют следующим образом: в декартовой системе координат
в цилиндрической системе координат
в сферической системе координат
Описание дифференциальных свойств векторного поля несколько сложнее. Векторное поле А принято характеризовать скалярным полем - дивергенцией div А и векторным полем - ротором rоt А. Значение дивергенции равно плотности источников рассматриваемого поля в заданной точке пространства. Трактовка ротора векторного поля сложнее, можно считать, что оно в известном смысле характеризует степень отличия исследуемого поля от однородного. Дивергенцию векторного поля А вычисляют путем дифференцирования его проекций по определенным правилам: в декартовой системе координат
в цилиндрической системе координат
в сферической системе координат
В произвольной ортогональной криволинейной системе координат
Проекции ротора векторного поля имеют вид: в декартовой системе координат
в цилиндрической системе координат
в сферической системе координат
Ротор векторного поля А в произвольной системе координат выражают через проекции исходного поля и коэффициенты Лямэ:
Дифференциальные операции со скалярными и векторными полями удобно записывать с помощью оператора Гамильтона
В декартовой системе координат оператор Гамильтона есть символический вектор
Из дифференциальных векторных операций второго порядка широкое применение в электродинамике находит оператор
Дифференциальная операция второго порядка, действующая на скалярное поле, задается оператором Лапласа
Оператор Лапласа в различных координатных системах записывается следующим образом: в декартовой системе координат
в цилиндрической системе координат
в сферической системе координат
Для графического изображения векторных полей принято строить картину их силовых линий. В каждой точке силовой линии вектор поля касательный к ней. Там, где интенсивность поля больше, силовые линии проводят чаще, и наоборот. § 1.2. Примеры решения типовых задач. 1.1. В декартовой системе координат проекции векторного поля А постоянны в каждой точке пространства:
Построить картину силовых линий векторного поля. Решение. Поскольку одна из декартовых составляющих векторного поля отсутствует, силовые линии должны представлять собой семейство плоских кривых, лежащих в плоскостях, параллельных плоскости ху. Вектор поля в каждой точке касателен к силовой линии, откуда вытекает дифференциальное уравнение силовых линий
являющееся следствием подобия двух прямоугольных треугольников с катетами dх, dу и А0, В0соответственно. Общий интеграл уравнения (1.16) имеет вид
где С - произвольная постоянная.
Рис.1.1 Рис.1.2 Таким образом, силовые линии поля представляют собой однопараметрическое семейство прямых с угловым коэффициентом наклона к оси х, равным В0 /А0 (рис. 1.1). 1.2. Векторное поле А, удовлетворяющее во всех точках рассматриваемой области условию div А = 0, называется соленоидальным (полем без источников). При выполнении условия rot А = 0 поле А является потенциальным векторным полем. Если такое поле характеризует силу, действующую на материальную точку, то работа внешних сил при обходе замкнутого контура будет равна нулю. В декартовой системе координат векторное поле А имеет единственную составляющую Проверить, является ли поле: а) соленоидальным; б) потенциальным. Решение. Картина силовых линий поля А в плоскости ху изображена на рис. 1.2. Вычисляя дивергенцию этого поля по формуле (1.2), получим, что div А = ∂Аy/∂y = 0. Следовательно, исследуемое поле соленоидально. Однако в соответствии c (1.6) rot А = 30х1z, поэтому поле не является потенциальным. 1.3. Вычислить дивергенцию векторного произведения полей А и В. Решение. Здесь удобно воспользоваться оператором Гамильтона, записав
Оператор Гамильтона является дифференциальным оператором, поэтому к приведенному векторному произведению можно применит обычные правила дифференцирования произведения:
Нижние индексы у оператора указывают поле, на которое он воздействует. Поле, на которое оператор не воздействует, должно быть вынесено за знак оператора подобно константе. В результате получаем
§ 1.3. Задачи для самостоятельного решения. 1.4. Скалярное поле φ задано в декартовой системе координат выражением
Вычислить векторное поле grad φ. Ответ: 1.5. В декартовой системе координат векторное поле А имеет единственную составляющую Аz = 3у2. Построить качественно пространственную картину распределения силовых линий поля. Вычислить векторное поле rot А. Ответ: 1.6. Пусть поле А предыдущей задачи характеризует векторы скоростей потока жидкости. В любую точку пространства может быть помещена миниатюрная “турбина” с прямыми лопатками (рис. 1.3); ориентация ее оси произвольна. Рис.1.3. Почему не будет вращаться “турбина”, помещенная в поток жидкости со скоростями, одинаковыми в каждой точке? Почему угловая скорость вращения равна нулю при 1.7. В сферической системе координат задано векторное поле Ответ: div А = 3. 1.8. В сферической системе координат векторное поле А имеет единственную r-ю составляющую, причем Ответ: 1.9. В декартовой системе координат скалярное поле φ имеет вид
где
Найти выражения для grad φ и Δφ. Ответ: 1.10.Определить дивергенцию и ротор векторного поля, имеющего в декартовой системе координат единственную составляющую Ответ: 1.11. Определить дивергенцию и ротор векторного поля А, характеризуемого следующими составляющими в цилиндрической системе координат: Ответ: 1.13. В декартовой системе координат некоторое скалярное поле задано трехмерным интегралом Фурье
Вычислить Δφ. Ответ: 1.14. Изобразить графически картину силовых линий векторных полей, заданных в декартовой системе координат своими проекциями:
1.15. Найти ротор и дивергенцию следующих векторных полей, заданных в декартовой системе координат:
Ответ: 1.16.Используя правила действия с оператором Гамильтона, доказать тождество
1.17. В пространстве заданы два векторных поля А и В. Найти выражение для поля Указание: Выразить операцию grad через оператор Ответ: 1.18. Доказать следующие тождества векторного анализа (φ и А - произвольные дифференцируемые скалярное и векторное поля):
1.19. Векторное поле А обладает единственной составляющей Ax, которая постоянна в пределах плоского слоя толщиной 2d:
Найти выражение ротора поля. Ответ: Литература 1.Лялин К.С., Приходько Д.В.Электродинамика СВЧ. Ч.1. – М.: МИЭТ, 2009, стр. 9 – 18. 2. Лялин К.С.,Антенно-фидерные устройства. Ч.1. – М.: МИЭТ, 2004, стр. 5 – 7. 3. Баскаков С.И. Электродинамика и распространение радиоволн. Сборник задач. – М. Высшая школа, 1981 г., глава 1. 4. Ефимов А.В.Математический анализ (специальные разделы). Учеб. пособие для вузов: В 2-х ч. Ч. 2: Применение некоторых методов математического и функционального анализа. - М.: Высшая школа, 1980. – 295 с.
Поиск по сайту: |
 скалярное поле φ приобретает вид некоторой функции
скалярное поле φ приобретает вид некоторой функции  принимающей численные значения - действительные или комплексные. Векторное поле А задается тремя проекциями на единичные векторы (орты) выбранной системы координат:
принимающей численные значения - действительные или комплексные. Векторное поле А задается тремя проекциями на единичные векторы (орты) выбранной системы координат: .
. , (1.1)
, (1.1) ,
,  ,
,  - коэффициенты Лямэ по координатам
- коэффициенты Лямэ по координатам  ,
, 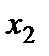 ,
,  являющиеся коэффициентами пропорциональности между дифференциалами обобщенных координат и бесконечно малыми ребрами элементарного параллелепипеда в выбранной точке пространства.
являющиеся коэффициентами пропорциональности между дифференциалами обобщенных координат и бесконечно малыми ребрами элементарного параллелепипеда в выбранной точке пространства. 
 ,
,  ,
, 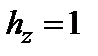
 ,
,  ,
, 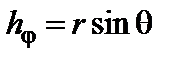 .
.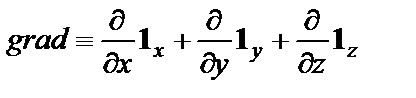 ;
; ;
; .
. ; (1.2)
; (1.2)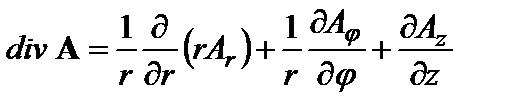 ; (1.3)
; (1.3) . (1.4)
. (1.4) (1.5)
(1.5) ,
, , (1.6)
, (1.6) .
. ,
, , (1.7)
, (1.7) ;
;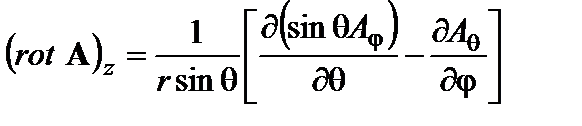 ,
, , (1.8)
, (1.8)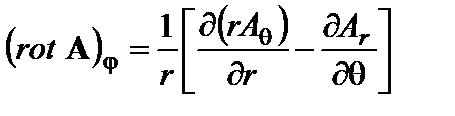 .
. (1.9)
(1.9) . По определению
. По определению ,
,  ,
,  . (1.10)
. (1.10) . (1.11)
. (1.11) , закон действия которого на векторное поле А описывается соотношением
, закон действия которого на векторное поле А описывается соотношением  . (1.12)
. (1.12) .
.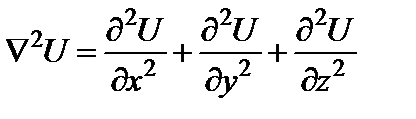 ; (1.13)
; (1.13)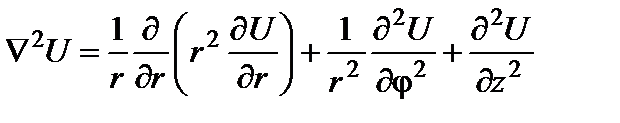 ; (1.14)
; (1.14) (1.15)
(1.15) ,
,  ,
,  .
. , (1.16)
, (1.16) ,
, .
. .
. .
.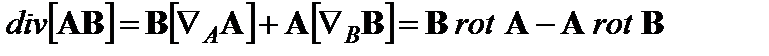 .
.
 .
.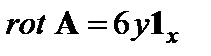 .
. и изменяет направление при переходе из области
и изменяет направление при переходе из области  в область
в область 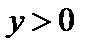 ? Установить связь этих результатов с математическим понятием ротора векторного поля как циркуляции по бесконечно малому контуру.
? Установить связь этих результатов с математическим понятием ротора векторного поля как циркуляции по бесконечно малому контуру.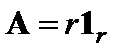 . Определить скалярное поле div A. Качественно построить картину силовых линий векторного поля.
. Определить скалярное поле div A. Качественно построить картину силовых линий векторного поля.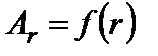 . Какова должна быть функция
. Какова должна быть функция  , чтобы дивергенция поля А обращалась тождественно в нуль? Построить картину силовых линий поля.
, чтобы дивергенция поля А обращалась тождественно в нуль? Построить картину силовых линий поля.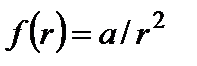 , где а - константа.
, где а - константа. ,
, мнимая единица;
мнимая единица;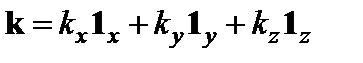 - постоянный вектор;
- постоянный вектор; - радиус-вектор.
- радиус-вектор.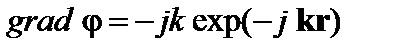 ,
, 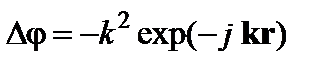 , где
, где  .
. .
.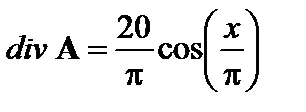 ,
,  .
. ,
,  ,
,  .
. ,
,  .
.
 ,
, .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, .
. ,
,  ,
,  ,
, 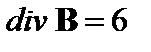 .
. .
. .
. и воспользоваться правилом дифференцирования произведения.
и воспользоваться правилом дифференцирования произведения. 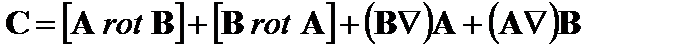 .
. ,
, ,
, ,
, ,
,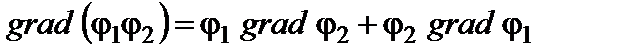 .
.
 , где
, где  - функция Дирака.
- функция Дирака.