Задачи для самостоятельного решения. 2.8.Показать, что векторное полеН, изменяющееся в пространстве и во времени по закону

2.8.Показать, что векторное полеН, изменяющееся в пространстве и во времени по закону

,

не может быть полем магнитного вектора, удовлетворяющим уравнениям Максвелла.

2.9.Показать, что из четвертого уравнения Максвелла в неоднородной среде, магнитная проницаемость которой есть функция пространственных координат, вытекает следующее уравнение для вектора напряженности магнитного поля:

.

2.10.Некоторый электромагнитный процесс характеризуется тем, что все составляющие полей зависят лишь от координаты z.

Показать, что на основании уравнений Максвелла при этом будут отсутствовать продольные составляющие Е_z и Н_z.

2.11.Показать, что электромагнитное поле, гармонически изменяющееся от времени с частотой ω в области пространства, свободной от источников, удовлетворяет однородным уравнениям Гельмгольца

.

2.12.Доказать, что четвертое уравнение Максвелла divВ = 0 можно рассматривать как следствие второго уравнения rotE= –∂В/∂t при некотором дополнительном условии. Каково это условие?

2.13.В материальной среде с параметрами ε=3,5 и σ=0,72 См/м создано электрическое поле, имеющее частоту 600 МГц и амплитуду 15 В/м.

Определить амплитудное значение и фазовый угол вектора плотности полного тока, существующего в каждой точке данной среды.

Ответ: J_Σ= 10,94 А/м2; ток опережает по фазе напряженность поля на угол 0,16 рад.

2.14.В толще однородного диэлектрика с известной относительной проницаемостью ε первоначально было создано равномерное электрическое поле Е, а затем прорезаны две узкие полости 1 и 2 (рис. 2.2), одна из которых ориентирована параллельно, а другая перпендикулярно полю. Полости заполнены воздухом.

Рис.2.2.

Какова величина напряженности электрического поля в обеих полостях?

Указание: воспользоваться граничными условиями для векторов электрического поля.

Ответ: если полость параллельна внешнему полю, то Е_внут = Е_внеш; в противном случае Е_внут = εЕ_внеш.

2.15.Исходя из результата предыдущей задачи объяснить, почему твердый диэлектрик, содержащий воздушные включения (пузырьки, каналы), будучи помещен в сильное электрическое поле, имеет меньшую электрическую прочность по сравнению с однородным диэлектриком.

2.16.В круглом цилиндрическом проводнике диаметром 2 мм существует постоянный ток величиной 7,5 А. Провод выполнен из меди.

Определить тангенциальную составляющую вектора напряженности электрического поля на поверхности провода.

Ответ: Е_τ=0,042В/м.

2.17.Бесконечно тонкий диск радиусом r₀, равномерно заряженный с плотностью σ_q, вращается вокруг оси с угловой скоростью Ω.

Определить вектор плотности поверхностного тока.

Ответ: η = ± σ_q Ω r 1_j; знак зависит от направления вращения.

2.18.Некоторый анизотропный диэлектрик имеет тензор относительной диэлектрической проницаемости, который в декартовой системе координат записывается таким образом:

.

В диэлектрике создано электрическое поле Е = 2,5 1_x + 1.7 1_y + 9,2 1_z.

Определить вектор электрической индукции D. Каков угол в пространстве между векторами E и D?

Ответ: D= ε₀(16,25 1_x + 11,05 1_y + 61,18 1_z,), Ð(DЕ) = 6,59⋅10^-3 рад.

2.19.В однородной проводящей среде с параметрами ε и σ в момент времени t = 0 создано начальное распределение плотности зарядов ρ₀(х, у, z).

Показать, что за счет токов проводимости в среде происходит экспоненциальное уменьшение плотности объемного заряда:

ρ (х, у, z, t) = ρ₀ехр [-σ/(εε₀)].

Оценить τ – характерное время релаксации этого процесса для типичного металла, у которого σ₁ = 10⁷ См/м, а также для полупроводника, имеющего σ² = 10^-3 См/м.

Указание: воспользоваться уравнением непрерывности.

Ответ: τ₁ ≈ 10^-18 с, τ₂ ≈ 10^-8 с.

2.20.Грозовая туча, имеющая площадь 5 км², располагается на высоте
2 км от поверхности Земли. Между тучей и Землей образуется постоянное электрическое поле с одинаковой во всех точках Е = 2⋅10⁵ В/м.

Оценить энергию поля.

Ответ: 1,77 · 10⁹ Дж..

2.21.По данным наблюдений, шаровая молния имеет диаметр порядка
20 см и содержит значительный запас энергии, зачастую превышающий энергию летящей винтовочной пули.

Может ли шаровая молния иметь только электрическую природу? Положить, что предельно допустимое значение напряженности электрического поля в воздухе Е = 30 кВ/см.

2.22.Сердечник трансформатора выполнен из стали с плотностью 7,7г/см³ и имеет массу 2 кг. Амплитудное значение магнитной индукции 2,1Тл, относительная магнитная проницаемость стали µ = 200.

Найти максимальное значение энергии, запасаемой в сердечнике, при намагничивании его синусоидальным током.

Ответ: 2,279 Дж.

2.23. *Конденсатор при t=0 начинает заряжаться от источника постоянной э. д. с. (рис. 2.3).

Рис.2.3.

Дать качественное описание процесса передачи энергии от источника в конденсатор. Как выглядят линии потока энергии в непосредственной близости от конденсатора?

2.24.Вектор напряженности электрического поля Ев декартовой системе координат имеет единственную составляющую Е_x, отличную от нуля.

Показать, что при этом вектор Пойнтинга не может иметь составляющей вдоль оси х.

2.25.В некоторой точке пространства вектор напряженности электрического поля Е=201_у В/м, в то время как вектор Пойнтинга

П = 101_х +301_z Вт/м².

Определить вектор напряженности магнитного поля.

Ответ: Н= -1,51_х + 0,51_z А/м.

2.26.В фиксированной точке пространства известны мгновенные значения векторов поля

,

,

где Е₀ иН₀–постоянные векторы.

Показать, что мгновенное значение вектора Пойнтинга складывается из неизменного во времени среднего значения

и колеблющейся части

,

изменяющейся во времени с удвоенной частотой.

2.27.В диэлектрике с проницаемостью ε = 2,4 создано постоянное электрическое поле напряженностью Е = 200 кВ/м.

Определить электрический дипольный момент области диэлектрика объемом 6 см³.

Ответ: 1,485⋅10¹¹Кл·м.

2.28. *При феноменологическом описании частотных свойств полярных диэлектриков используют математическую модель, которая уподобляет молекулярные диполи воображаемым твердым частицам, испытывающим при своем движении вязкое сопротивление окружающей среды. При этом связь между вектором поляризованности Р и вектором напряженности электрического поля Е устанавливается дифференциальным уравнением

,

где а — константа; Т — время релаксации среды.

Вывести зависимость комплексной абсолютной диэлектрической проницаемости от частоты.

Ответ: .

2.29.Используя условия предыдущей задачи, вывести формулу, определяющую тангенс угла диэлектрических потерь.

Ответ:.

2.30. *Решить задачу 2.28 для случая, когда динамика процесса поляризации описывается уравнением

,

где ω₀ — собственная частота молекулярного диполя; b — константа. Такое уравнение возникает, если в качестве модели диполя принять осциллятор с трением.

Проанализировать графики частотных зависимостей действительной и мнимой частей диэлектрической проницаемости.

Ответ: .

2.31.Комплексная амплитуда вектора напряженности электрического поля

(углы даны в радианах). Частота колебаний 2 МГц.

Найти мгновенное значение вектора Е в момент времени, равный 0,1мкс.

Ответ:

2.32.Комплексные амплитуды векторов электромагнитного поля в некоторой точке пространства задаются выражениями

,

Определить комплексный вектор Пойнтинга и его среднее значение.

Ответ:

Литература

1.Лялин К.С., Приходько Д.В.Электродинамика СВЧ. Ч.1. – М.: МИЭТ, 2009., стр. 9 – 28.

Поиск по сайту:
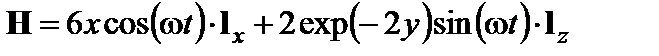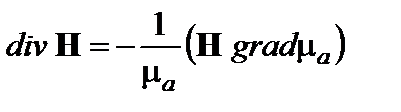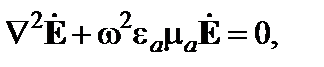
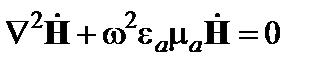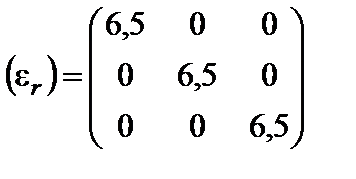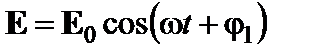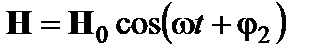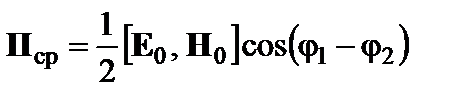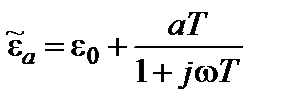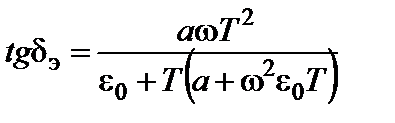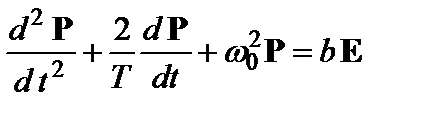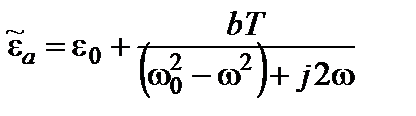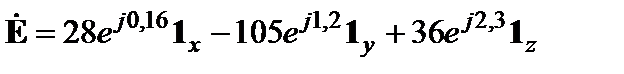
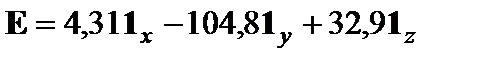
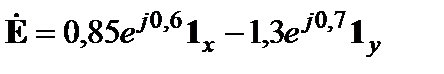