 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Классическое определение вероятности. Основным понятием теории вероятностей является понятие случайного события
Основным понятием теории вероятностей является понятие случайного события. Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием. Событие называется достоверным, если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может. Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе. Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними. Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами. Исход называется благоприятствующим появлению события А, если появление этого события влечет за собой появление события А. Пример. В урне находится 8 пронумерованных шаров (на каждом шаре поставлено по одной цифре от 1 до 8). Шары с цифрами 1, 2, 3 красные, остальные – черные. Появление шара с цифрой 1 (или цифрой 2 или цифрой 3) есть событие, благоприятствующее появлению красного шара. Появление шара с цифрой 4 (или цифрой 5, 6, 7, 8) есть событие, благоприятствующее появлению черного шара. Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу Свойство 1. Вероятность достоверного события равна единице Итак, вероятность любого события удовлетворяет двойному неравенству Пример. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10? Решение. Пусть событие А = (Номер вынутого шара не превосходит 10). Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m=n=10. Следовательно, Р(А)=1. Событие А достоверное. Пример. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые? Решение. Вынуть два шара из десяти можно следующим числом способов: Пример. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар? Решение. Так как синих шаров в урне нет, то m=0, n=15. Следовательно, искомая вероятность р=0. Событие, заключающееся в вынимании синего шара, невозможное. Пример. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты червовой масти? Решение. Количество элементарных исходов (количество карт) n=36. Событие А = (Появление карты червовой масти). Число случаев, благоприятствующих появлению событияА, m=9. Следовательно, Пример. В кабинете работают 6 мужчин и 4 женщины. Для переезда наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины. Решение. Общее число возможных исходов равно числу способов, которыми можно отобрать 7 человек из 10, т.е. Найдем число исходов, благоприятствующих интересующему нас событию: трех женщин можно выбрать из четырех Искомая вероятность Текст задания: Задача 1. Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места. Задача 2.Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры. Задача 3. Шесть шаров случайным образом раскладывают в три ящика. Найти вероятность того, что во всех ящиках окажется разное число шаров, при условии, что все ящики не пустые. Задача 4. На шахматную доску случайным образом поставлены две ладьи. Какова вероятность, что они не будут бить одна другую? Задача 5. Шесть рукописей случайно раскладывают по пяти папкам. Какова вероятность того, что ровно одна папка останется пустой? Задача 6. Цифры 1, 2, 3, …, 9, выписанные на отдельные карточки складывают в ящик и тщательно перемешивают. Наугад вынимают одну карточку. Найти вероятность того, что число, написанное на этой карточке: а) четное; б) двузначное. Задача 7. На полке в случайном порядке расставлено 40 книг, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания номера слева направо, но не обязательно рядом. Задача 8. На каждой из пяти одинаковых карточек напечатана одна из следующих букв: "а", "м", "р", "т", "ю". Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово "юрта". Задача 9. Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова вероятность того, что ребенок соберет из кубиков слово "кукла"?
Поиск по сайту: |
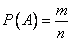
 .
.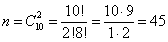 .
.  .
. 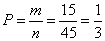 .
. .
. .
. способами; при этом остальные четыре человека должны быть мужчинами, их можно отобрать
способами; при этом остальные четыре человека должны быть мужчинами, их можно отобрать  способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно  .
.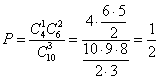 .
.