 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Практическая работа № 11
Тема: Тригонометрические функции их графики и свойства Цель работы: закрепить знания и умения студентов по освоению свойств тригонометрических функций. Теоритическое обоснование: Функции y = sin x, y = cos x, y = mf(x), y = f(kx), y = tg x, y = ctg x
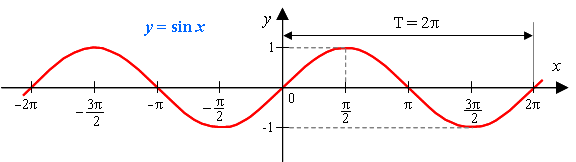
Функция y = sin x Графиком функции является синусоида. Полную неповторяющуюся часть синусоиды называют волной синусоиды. Половину волны синусоиды называют полуволной синусоиды (или аркой).
Для построения графика функции y = sin x удобно применять следующие масштабы: - на листе в клетку за единицу отрезка примем длину в две клетки. - на оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π. Это значения x. - на оси y отметим 1, включающий две клетки. Составим таблицу значений функции, применяя наши значения x:
Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1). Это график функции y = sin x на отрезке [0; π]. Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна. Это график функции y = sin x на отрезке [-π; π]. Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами. Функция y = cos x.
Графиком функции является синусоида (ее иногда называют косинусоидой).
Свойства функции y = cos x:
Функция y = mf(x). Возьмем предыдущую функцию y = cos x. Как вы уже знаете, ее графиком является синусоида. Если мы умножим косинус этой функции на определенное число m, то волна растянется от оси x (либо сожмется, в зависимости от величины m). Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m. Если m < 1, то синусоида сжимается к оси x на коэффициент m. Если m > 1, то синусоида растягивается от оси x на коэффициент m. Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график. Функция y = f(kx). Если функция y = mf(x) приводит к растяжению синусоиды от оси x либо сжатию к оси x, то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y. Причем k – любое действительное число. При 0 < k < 1 синусоида растягивается от оси y на коэффициент k. Если k > 1, то синусоида сжимается к оси y на коэффициент k. Составляя график этой функции, можно сначала построить одну полуволну синусоиды, а по ней достроить затем весь график. Функция y = tg x.
Графиком функции y = tg x является тангенсоида. Достаточно построить часть графика на промежутке от 0 до π/2, а затем можно симметрично продолжить ее на промежутке от 0 до 3π/2.
Свойства функции y = tg x:
Функция y = ctg x
Графиком функции y = ctg x также является тангенсоида (ее иногда называют котангенсоидой).
Свойства функции y = ctg x:
Текст задания:
Поиск по сайту: |



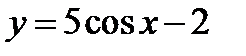
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 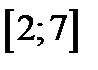
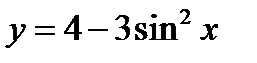
 2)
2)  3)
3) 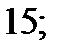 4)
4) 

 2)
2)  3)
3)  4)
4) 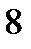

 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 

 2)
2)  3)
3) 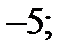 4)
4) 

 3)
3) 

 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 

 2)
2)  3)
3)  4)
4) 
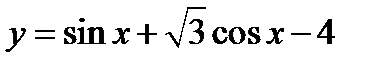
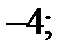 2)
2)  3)
3) 
 ; 3)
; 3)  ; 4)
; 4) 

 2)
2)  3)
3) 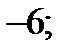 4)
4) 

 2)
2)  3)
3) 