 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
П.4.Кинематические характеристики для движения МТ по окружности ⇐ ПредыдущаяСтр 7 из 7
Звук При анализе движения твердых тел мы увидим, что особое место занимает вращение тела, когда все его точки движутся по окружностям. Мы должны быть к этому готовы. Проблема: Найти особые кинематические характеристики движения МТ по окружности. При движении МТ по окружности траектория движения уже определена и однозначно задается радиусом окружности и положением окружности в пространстве. Начало системы координат обычно совмещают с центром окружности. Замечание: Поскольку оси декартовой системы координат образуют правую тройку векторов, то это означает, что, если рукоятку винта вращать от оси Х к оси Y, то стержень винта пойдет по оси Z. Это следует помнить, когда вы делаете соответствующий рисунок.
Кинематическими характеристиками МТ, движущейся по окружности, являются 1. j - угол от положительного направления оси Х до радиус-вектора. При движении угол меняется: j(t) – закон движения. 2. Направление Математически определение модуля угловой скорости выглядит так:
3. Угловое ускорение
Замечание: Если
Звук
ЗАДАЧА: Найти закон движения при движении по окружности, плоскость которой неподвижна. РЕШЕНИЕ: Из определения углового ускорения находим приращение угловой скорости Из определения угловой скорости
ЧАСТНЫЙ СЛУЧАЙ: Если угловая скорость постоянна как по величине, так и по направлению, т.е. Пусть задано угловое ускорение. Плоскость неподвижна. Выражение для угловой скорости найдем из определения углового ускорения
w(t’) = w0 + Закон движения тогда
j(t) = j0 + = j0 + = j0 + w0 t + Замечание: Кроме углового ускорения, необходимо задавать два начальных условия (начальный угол и начальную угловую скорость).
Поиск по сайту: |
Z
– угловая скорость, есть быстрота изменения угла j со временем.
.
- угловое ускорение показывает как быстро и в каком направлении меняется вектор 
.
, то 
dt, т.е. приращение 
находим приращение угла 
. Далее интегрируем слева и справа: 
или 
, отсюда j(t) = j0 + 
- ответ для случая, когда задана угловая скорость.
= const, ее модуль w можно вынести за знак интеграла. Тогда получим j(t) = j0 + wt – частный случай закона движения для движения с постоянной угловой скоростью (называется – равномерное вращение).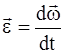
, отсюда 
не меняется), то dw = e dt. Интегрируем слева и справа
и получаем
.
+ 
=