 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
П.4.Модели материальная точка (МТ) и мгновенное событие (МС)
Звук Проблема: Реальный материальный объект чрезвычайно (практически бесконечно) сложен. Как же его исследовать, ведь у него бесконечно много характеристик? Решение: Заменить объект некоторой упрощенной конструкцией, которая называется моделью. В жизни мы часто используем термин модель, например, для модели самолета, которую вам подарили на день рождения. Пластмассовая модель самолета в качестве общего с реальным самолетом имеет только форму. Далее мы будем использовать термины, содержание которых может в определенной степени отличаться от того, которое принято в обыденной жизни. Модель – абстрактная конструкция, существующая только у нас в голове, но в определенной степени «привязанная» к реальному материальному объекту: модель имеет часть характеристик моделируемого объекта, а остальными характеристиками «пренебрегают», т.е. обычно считают, что их нет (равны нулю). Наиболее простыми являются модели материальная точка и мгновенное событие. Материальная точка – это абстрактный объект, не имеющий размеров, но имеющий другие характеристики моделируемого объекта. Применяется для описания реальных объектов, размерами которых можно пренебречь в условиях данной задачи (частицы). Мгновенное событие – абстрактный процесс, имеющий нулевую длительность, применяемый для описания реальных процессов, длительностью которых можно пренебречь в условиях данной задачи.
У одного и того же объекта может быть несколько моделей: все зависит от условия задачи. Пример 1: Какова модель планеты под названием Земля. Модель – глобус? Вы так считаете! В какой-то степени – да. Для определенных целей ее можно использовать, например, чтобы посмотреть, где живем мы, а где австралийцы. Но для физики не подходит. Если процесс – это движение вокруг Солнца, то Земля – материальная точка (МТ). Если процесс – это вращение Земли вокруг оси, то модель – абсолютно твердое тело (АТТ).
Пример 2: Электромагнитное излучение (то, с помощью чего мы существуем) описывается с помощью трех моделей 1.Луч (модель геометрической оптики). 2.Волна (модель физической оптики, радиотехники и всего, что на ней построено). 3.Поток частиц - фотонов (модель квантовой оптики).
Замечание: Электромагнитное излучение – часть единой совокупности, которая называется материей. Оно передает электромагнитное взаимодействие. Тема 2. Системы отсчета.
П.1.Вектор Звук Проблема: Какой математический объект надо использовать для описания физической характеристики, имеющей не только величину, но и направление в пространстве? Решение: Вектор – направленный отрезок в пространстве. Изобразим вектор на рисунке. Рядом с вектором принято писать символ, над которым нарисована стрелка.
Любая физическая характеристика, имеющая направление в пространстве, называется векторной. Ее описывают с помощью матерматического объекта, называемого вектором. Некоторые общепринятые обозначения:
Вектор – это длина + направление. Длина = число + (единица измерения). Проблема: Как описать направление? Из математики: Проекция – длина отрезка (со знаком) между основанием перпендикуляров, опущенных из концов вектора на данную ось.
Ay О Аx a x AZ b z Проблема: Как определить знак проекции? Изобразим на рисунке вектор
А +, если вектор с осью составляет острый угол a –, если угол тупой a O 14243 X AX Если вектор расположен в плоскости, тогда вектор есть совокупность двух чисел: либо а проекции выражаются через модуль вектора и углы так
AX = A Cos(a), AY = A Sin(a).
Звук
Основные операции с векторами
Рассмотрим правила сложения и вычитания:
т.е. складываются (вычитаются) соответствующие проекции векторов.
Теперь перейдем к операции умножения. Умножить вектор на число значит умножить на это число его модуль. В координатном представлени на число надо умножить каждую проекцию вектора.
Существуют два способа умножения векторов друг на друга: 1.Скалярное
2.Векторное
Изобразим на рисунке три вектора, связанные векторным произведением. Пусть векторы
Z
Свойства векторного произведения: 1. С = AB Sin(a), где a - угол между сомножителями, 2. Результирующий вектор ортогонален каждому сомножителю:
Для определения направления векторного произведения используют правило правого винта: Рукоятка винта поворачивается от первого вектора ко второму. Движение стержня винта показывает направление третьего вектора (произведения). В нашем случае первый вектор это Замечание: Векторным произведением связаны единичные векторы (орты) осей координат : Оба варианта произведения векторов очень часто встречаются в физических законах. Мы это увидим далее. П.2.Производная. Звук Проблема: Как измерять быстроту изменения какой-либо характеристики? Решение: (предложил Ньютон) Надо использовать дифференциал - бесконечно малое приращение.
Сначала рассмотрим простое изменение (приращение) некоторой характеристики А: По определению ∆А = АКОН – АНАЧ . Предельный переход от конечных к бесконечно малым: ∆ ® d. Например, ∆t ® dt (как t обозначаем время). Кроме того всегда принято обозначать: ∆ (читается «дельта») – конечное приращение, d – бесконечно малое приращение, lim (читается «лимит») º предел.
Обозначим функцию y = f(t). Тогда быстрота изменения характеристики y со временем t есть приращение y , деленное на приращение времени, при условии, что приращение времени стремится к нулю. Это записывается, как предел Замечание: В школе производная почему-то обозначается, как f¢ или y¢. Функция – как y, а ее аргумент, как x. Графически:
Δy b tga – тангенс угла для секущей y a
t t Δt касательная При Dt ® 0 имеем a ® b и
Таким образом производная численно равна тангенсу угла наклона к горизонтальной оси касательной, проведенной в данной точке графика. Ответ: Быстрота изменения некоторой характеристики А со временем есть производная от этой характеристики по времени, т.е. СРС 1 (1/2 страницы): Запишите формулы производных от основных функций и правила дифференцирования.
Поиск по сайту: |


 А
А

 А – величина (модуль) ≡А
А – величина (модуль) ≡А  = {A, a, b} - тройка чисел, например,
= {A, a, b} - тройка чисел, например,  y
y , направленный под некоторым углом a к горизонтальной оси Х.
, направленный под некоторым углом a к горизонтальной оси Х. Y
Y

 ¿
¿ .
.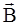 расположены в горизонтальной плоскости XZ, тогда вектор
расположены в горизонтальной плоскости XZ, тогда вектор  будет направлен по вертикальной оси Y.
будет направлен по вертикальной оси Y.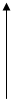 U
U



 Х
Х



 a
a
 и
и  .
.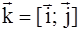 .
. , который в математике сокращенно записывается так
, который в математике сокращенно записывается так  и называется «производная от f (или от y) по t».
и называется «производная от f (или от y) по t». y y = f(t)
y y = f(t) превращается в
превращается в .
. . Быстрота изменения некоторой характеристики А в пространстве есть производная от этой характеристики по координате (например, по х), т.е.
. Быстрота изменения некоторой характеристики А в пространстве есть производная от этой характеристики по координате (например, по х), т.е.  .
.