 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
П.5.Преобразование Лоренца для длины отрезка
Звук Проблема: Как связаны результаты измерения размеров тела, выполненные в разных СО. Пусть объект движется. Простейший объект, имеющий размеры, это отрезок. Простейшие измерения в СО, где отрезок неподвижен. Для СО, где отрезок движется, есть проблема однозначности измерения его длины. Решение проблемы: измерения координат концов отрезка надо производить одновременно (Dt’= 0), а затем вычесть из одной координаты другую. Пусть отрезок расположен вдоль Х:
Y¢ K¢ vo K X¢ X Используем формулу преобразований Лоренца для координат, куда справа входит Dt (чтобы использовать потом условие Dt = 0): Dx’ = Г(Dх – V0Dt), отсюда При движении длина отрезка уменьшается в Г раз. Принято говорить, что “при движении отрезок сокращается”. Полная формулировка результата исследования: Результат измерения длины отрезка в той СО, где он движется (Dx) будет меньше в Г раз меньше, чем в той СО, где он неподвижен (Dx’). Максимальной длиной отрезок обладает в той СО, где он неподвижен (собственная СО отрезка).
Задача. Пусть неподвижный отрезок направлен под углом a0 . Что произойдет при его движении? В СО К’ отрезок будет неподвижен, поэтому его угол a’ = a0 , а в СО К у отрезка будет новый угол a .
Y Y’ X’ vo a’ X Dy’ = Dy и Dx’ = Г Dx.
Окончательно a ³ a0 . Напомним, что штрих ставится в той системе отсчета, где отрезок покоится. Ответ: при движении отрезок сокращается и поворачивается, приближаясь к вертикали. П.6.Преобразования Лоренца для скорости Звук Проблема: Как связаны результаты измерения скорости МТ, если измерения проведены в разных движущихся СО? Решение: Для простоты будем считать, что система К’ имеет параллельные К оси и движется вдоль оси Х со скоростью VО .
Используем преобразования Лоренца и определение проекции скорости:
Следствие: Величина скорости не может быть больше скорости света. Если v’ = c, то и v = c при любой скорости движения системы отсчета. Замечание: В отличие от поперечных компонент радиус-вектора, поперечные компоненты скорости будут разными при измерении в движущихся СО.
Полезная приближенная формула преобразования скоростей:
Поиск по сайту: |
– есть преобразование Лоренца для длины отрезка.
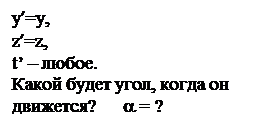
, поделим эти уравнения друг на друга: 
, отсюда
или 
³ 
- формула преобразования Лоренца для продольной компоненты скорости.
.
.