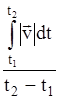|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
П.3.Движение с постоянным ускорением
Звук Проблема: Можно ли достаточно просто найти закон движения для какого-либо полезного случая? Решение: В качестве «простого и полезного» случая можно рассмотреть движение с постоянным ускорением. Определение: Равнопеременным называется движение с постоянным ускорением.
Задача: Исследовать движение с постоянным ускорением. Запишем это условие:
Записываем основные кинематические характеристики:
Суммирование элементарных приращений скорости есть интегрирование:
Далее из определения скорости выделим приращение радиус-вектора Для получения закона движения
Вынося константы за знак интегрирования и вычислив простейшие интегралы, получим
где Это и есть хорошо известная из курса школы формула, которую теперь мы честно вывели и будем далее называть законом движения МТ для случая постоянного ускорения.
Замечание: Для однозначного предсказания закона движения МТ недостаточно задать одно ускорение, а надо дополнительно задавать еще и начальное положение, и начальную скорость МТ. Тема 2. Дополнительные кинематические характеристики. Движение МТ по окружности
П.1.Траектория Звук Проблема: Как визуально можно представить движение?
Траекторией называется геометрическое место точек, которые последовательно занимает МТ при своем движении. Траектория это линия, изображающая движения.
X
Алгоритм получения уравнения траектории: · записать закон движения, · спроектировать его на оси системы координат, т.е. записать каждую проекцию радиус-вектора, как функцию времени, · устранить время из этих уравнений , · получить указанную функцию. Замечание: Траектория не единственный способ визуализации движения. Можно использовать график зависимости координаты от времени, например, x(t). Пример 1: Рассмотрим движение по окружности.
y МТ
0 x X
Получили уравнение траектории.
Пример 2. МТ движется в плоскости XY, причем закон движения выглядит так Решение. Используем известный нам алгоритм. В данной задаче. Закон движения задан через задание проекций радиус-вектора. Из заданного закона движения можно найти проекции x(t) = b×t и y(t) = c×t2. Решаем систему уравнений. Чтобы устранить время, надо из первого уравнения выразить t =
Это есть уравнение параболы. П.2. Путь. Средняя скорость. Звук Мы часто встречаем утверждения типа «Объект проделал такой-то путь» или «Мы проехали путь (почти 200 км) от Москвы до Твери со скоростью 100 км/час, а показания спидометра иногда доходили до 150 км/час». Вопрос: Что такое путь и как его вычислять с помощью известных кинематических характеристик? О какой скорости шла речь и что показывает спидометр автомобиля? Путь есть сумма длин отрезков траектории, на которых движение происходило в одном направлении. Если на некотором участке тело останавливается и начинает двигаться в другом направлении, тогда надо суммировать отрезки траектории с однонаправленным движением. Обозначения: dS – элемент пути, S – путь при однонаправленном движении является суммой элементарных путей S = å dS. Для бесконечно малых Используем определение скорости
Путь Окончательно
Средней скоростью называется отношение пути, пройденного телом, к промежутку времени, за который этот путь пройден. <v> = Получим формулы для вычисления средней скорости.
Замечание:Путь численно равен площади под кривой зависимости модуля скорости от времени v(t) между вертикальными линиями, проведенными при t1 и t2 .
На первую часть вопроса, поставленного в начале пункта, мы уже ответили. Теперь ответим и на вторую. Спидометр это специальный прибор, который измеряет модуль мгновенной скорости автомобиля. Одновременно он вычисляет и показывает на табло и путь, пройденный автомобилем, начиная с момента начала его эксплуатации. На некоторых спидометрах есть и еще одно табло, показывающее путь, пройденный с момента обнуления его показаний (так называемый «дневной пробег»).
Поиск по сайту: |

 (t),
(t),  ,
,  . Из последнего соотношения d
. Из последнего соотношения d  =
= 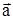 dt.
dt.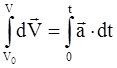 после интегрирования с учетом
после интегрирования с учетом  :
: 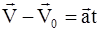 . Отсюда можно получить закон скорости для движения с постоянным ускорением
. Отсюда можно получить закон скорости для движения с постоянным ускорением  .
.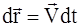 .
.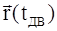 надо проинтегрировать это выражение:
надо проинтегрировать это выражение: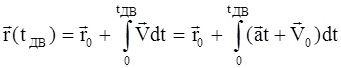 .
.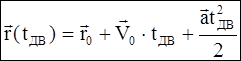 ,
,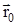 и
и 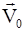 - начальное положение и начальная скорость МТ.
- начальное положение и начальная скорость МТ.

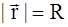
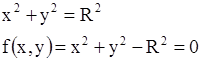
 , где b и с есть константы. Найти траекторию.
, где b и с есть константы. Найти траекторию.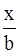 и подставить во второе
и подставить во второе 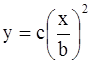 , отсюда
, отсюда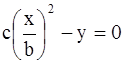 - есть искомое уравнение траектории.
- есть искомое уравнение траектории. .
.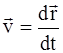 :
: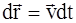 или
или 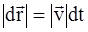 .
.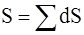 или
или 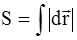 .
.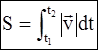 .
.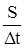 .
.
 <v> =
<v> =