 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
П.1.Движение с малой скоростью
Звук Очень важной проблемой является установление связи между результатами измерения физических характеристик в разных системах отсчета. Одни измерения могут проводиться в Москве, а другие – в Нью-Йорке. Проблема: Одна система отсчета движется относительно другой. Дадут ли измерения в них одинаковые результаты? Рассмотрим две системы отсчета с параллельными осями, из которых одну будем считать неподвижной, а другую – движущейся вдоль оси Х со скоростью
y¢ K¢
К
0 x Не трудно видеть, что Задача: Связать результаты измерения скорости, выполненные в разных движущихся системах отсчета. Надо знать, что происходит с результатами измерения времени. Предположим, что измерение времени в обеих системах дает одинаковый результат: t’ = t . Следовательно, тогда и dt’ = dt. Это требует проверки и подтверждения. Как известно, в обычной жизни это выполняется: измерение времени дает одинаковый результат как при измерении на земле, так и в самолете, поезде, ракете и т.д. Нет надобности перестраивать часы, если ты садишься в поезд. Тогда дифференцирование по t (деление на dt) можно заменить дифференцированием по t’ (делением на dt’) и получим или Преобразования Галилея: Для координат Вывод: Измерения в двух движущихся СО дают разные результаты как для радиус-вектора, так и для скорости МТ. Однако существуют простые соотношения, называемые преобразованиями Галилея, которые связывают результаты таких измерений. П.2.Скорость света. Звук Проблема: Всегда ли справедливы преобразования Галилея? Решение: Если мы не обнаруживаем противоречий, используя эти преобразования, то мы признаем их справедливыми всегда, до тех пор, пока не наталкиваемся на противоречия с действительностью.
К сожалению такое столкновении теории с действительностью произошло в начале 20 века. Полученная формула преобразования скоростей не обеспечивает ограничения величины скорости: скорость может быть любой, как у МТ, так и у систем отсчета. Это противоречит результатам некоторых экспериментов.
Экспериментально было обнаружено, что существует по крайней мере материальный объект (свет), скорость которого одинакова в любой инерциальной системе отсчета, включая и движущиеся. Затем теоретически было показано (Эйнштейн), что скорость любого материального объекта имеет предельное значение.
По современным представлениям скоростью света называется предельная скорость движения любого материального объекта. Обозначение: с = 3×108 м/с .
Был обнаружен по крайней мере один объект, скорость которого точно равна скорости света – это электромагнитное излучение, распространяющееся в вакууме. Скорость света численно равна скорости электромагнитной волны в вакууме. Замечание: Термин «свет» имеет историческое происхождение, так же, как и «скорость света». Мы же должны помнить точные физические определения, в частности, "Свет" – это частный случай электромагнитного излучения, которое видит человеческий глаз. И то, что «свет распространяется со скоростью света» это вовсе не тавтология, и требует экспериментального и теоретического подтверждения.
Поиск по сайту: |
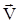 НО
НО = const.
= const.

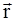 x¢
x¢ но
но .
. ,
, это и есть формула преобразования скоростей.
это и есть формула преобразования скоростей. , для времени t’ = t , для скоростей
, для времени t’ = t , для скоростей  В начале 20-го века были проведены эксперименты Майкельсона по измерению скорости света в разных направлениях по отношению к движению Земли. Скорость оказалась одной и той же.
В начале 20-го века были проведены эксперименты Майкельсона по измерению скорости света в разных направлениях по отношению к движению Земли. Скорость оказалась одной и той же.