 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие релятивистской массы
После того, как Эйнштейн предложил принцип эквивалентности массы и энергии, стало очевидно, что понятие массы может использоваться двояко. С одной стороны, это та масса, которая фигурирует в классической физике, с другой — можно ввести так называемую релятивистскую массу как меру полной (включая кинетическую) энергии тела[2]. Эти две массы связаны между собой соотношением:
где
Аналогичное соотношение выполняется для классических импульса и массы, что также приводится как аргумент в пользу введения понятия релятивистской массы. Введённая таким образом релятивистская масса в дальнейшем привела к тезису, что масса тела зависит от скорости его движения[11]. В процессе создания теории относительности обсуждались понятия продольной и поперечной массы частицы. Пусть сила, действующая на частицу, равна скорости изменения релятивистского импульса. Тогда связь силы
Если скорость перпендикулярна силе, то Утверждение о том, что масса зависит от скорости, вошло во многие учебные курсы и в силу своей парадоксальности приобрело широкую известность среди неспециалистов. Однако в современной физике избегают использовать термин «релятивистская масса», используя вместо него понятие энергии, а под термином «масса» понимая массу покоя. В частности, выделяются следующие недостатки введения термина «релятивистская масса»[3]: § неинвариантность релятивистской массы относительно преобразований Лоренца; § синонимичность понятий энергия и релятивистская масса, и, как следствие, избыточность введения нового термина; § наличие различных по величине продольной и поперечной релятивистских масс и невозможность единообразной записи аналога второго закона Ньютона в виде
§ методологические сложности преподавания специальной теории относительности, наличие специальных правил, когда и как следует пользоваться понятием «релятивистская масса» во избежание ошибок; § путаница в терминах «масса», «масса покоя» и «релятивистская масса»: часть источников просто массой называют одно, часть — другое. Несмотря на указанные недостатки, понятие релятивистской массы используется и в учебной[12], и в научной литературе. Следует, правда, отметить, что в научных статьях понятие релятивистской массы используется по большей части только при качественных рассуждениях как синоним увеличения инертности частицы, движущейся с околосветовой скоростью.
17. Законы сохранения энергии и импульса в СТО. 18. Колебания в механике. Упругие и квазиупругие силы. Собственные колебания. Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку. Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии. Классификация Выделение разных видов колебаний зависит от подчёркиваемых свойств колеблющихся систем (осцилляторов) [править]По физической природе § Механические (звук, вибрация) § Электромагнитные (свет, радиоволны, тепловые) § Смешанного типа — комбинации вышеперечисленных [править]По характеру взаимодействия с окружающей средой § Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явлениерезонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия. § Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити. § Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от свободных колебаний является, то что их амплитуда определяется свойствами самой системы, а не начальными условиями. § Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия. § Случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом. Характеристики § Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, § Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), § Частота — число колебаний в единицу времени, Период колебаний
В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота
§ Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения метр. § Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.
КВАЗИУПРУГАЯ СИЛА - направленная к центру О сила. модуль к-рой пропорционален расстоянию r от центра О до точки приложения силы (F=-cr), где с - постоянный коэф., численно равный силе, действующей на единице расстояния. К. с. является силой центральной и потенциальной с силовой ф-цией U=-0,5cr2. Примерами К. с. служат силы упругости, возникающие при малых деформациях упругих тел (отсюда и сам термин "К. с."). Приближённо К. с. можно также считать касательную составляющую силы тяжести, действующей на матем. маятник при малых его отклонениях от вертикали. Для материальной точки, находящейся под действием К. с., центр О является положением её устойчивого равновесия. Выведенная из этого положения точка будет в зависимости от нач. условий или совершать около О прямолинейные гармонич. колебания, или описывать эллипс (в частности, окружность). Си́ла упру́гости — сила, возникающая при деформации тела и противодействующая этой деформации. В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. В простейшем случае растяжения/сжатия тела сила упругости направлена противоположно смещению частиц тела, перпендикулярно поверхности. Вектор силы противоположен направлению деформации тела (смещению его молекул). [править]Закон Гука Основная статья: Закон Гука В простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид:
где В словесной формулировке закон Гука звучит следующим образом: Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации. [править]Нелинейные деформации При увеличении величины деформации закон Гука перестаёт действовать, сила упругости начинает сложным образом зависеть от величины растяжения или сжатия. Собственные колебания, свободные колебания, колебания в механической, электрической или какой-либо другой физической системе, совершающиеся при отсутствии внешнего воздействия за счёт первоначально накопленной энергии (вследствие наличия начального смещения или начальной скорости). Характер Собственные колебания определяется главным образом собственными параметрами системы (массой, индуктивностью, ёмкостью, упругостью). В реальных системах вследствие рассеяния энергии Собственные колебания всегда затухающие, а при больших потерях они становятся апериодическими. 19. Уравнения движения простейших механических колебательных систем без трения. Колебательная система — физическая система, в которой могут существовать свободные колебания 20. Энергия колебательной системы. 21. Свободные колебания. Уравнение движения колебательных систем с жидким трением. 22. Коэффициент затухания. Логарифмический декремент. Добротность. Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и (рис. 3.1):
Рис. 3.1 Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:
Выясним физический смысл χиβ. Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.
Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз. Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда
Если χ = 0,01, то N = 100. При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому , ато круговая частота обращается в нуль (w=0 ), а ( t- ), колебания прекращаются. Такой процесс называетсяапериодическим (рис. 3.2).
Рис. 3.2 Отличия в следующем. При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения. Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания. Общая формула для добротности любой колебательной системы:
где: § § §
23. Вынужденные колебания. Резонанс. Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени. Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частотаопределяются внутренними свойствами самой автоколебательной системы.
Поиск по сайту: |

 — релятивистская масса, m — «классическая» масса (равная массе покоящегося тела), v — скорость тела. Введённая таким образом релятивистская масса является коэффициентом пропорциональности между импульсом и скоростью тела[2]:
— релятивистская масса, m — «классическая» масса (равная массе покоящегося тела), v — скорость тела. Введённая таким образом релятивистская масса является коэффициентом пропорциональности между импульсом и скоростью тела[2]:
 и ускорения
и ускорения  существенно изменяется по сравнению с классической механикой:
существенно изменяется по сравнению с классической механикой:
 а если параллельна, то
а если параллельна, то  где
где  — релятивистский фактор. Поэтому
— релятивистский фактор. Поэтому  называют продольной массой, а
называют продольной массой, а  — поперечной.
— поперечной.
 (м)
(м) (с)
(с)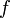 (Гц, с−1).
(Гц, с−1). и
и 
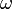 (рад/с, Гц, с−1), показывающая число колебаний за
(рад/с, Гц, с−1), показывающая число колебаний за 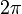 единиц времени:
единиц времени:
 ,
,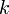 — жёсткость тела,
— жёсткость тела,  — величина деформации .
— величина деформации . где β– коэффициент затухания.
где β– коэффициент затухания.


 Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.
Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.
 ,
,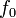 — резонансная частота колебаний
— резонансная частота колебаний — энергия, запасённая в колебательной системе
— энергия, запасённая в колебательной системе — рассеиваемая мощность.
— рассеиваемая мощность.