|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Преобразования Лоренца в физике
Преобразованиями Лоренца в физике, в частности, в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца. Преобразования Лоренца без сдвигов начала отсчёта образуют группу Лоренца, со сдвигами — группу Пуанкаре, иначе называемую неоднородной группой Лоренца. С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства. Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени. § Следует заметить, что лоренц-ковариантны не только фундаментальные уравнения (такие, как уравнения Максвелла, описывающее электромагнитное поле, уравнение Дирака, описывающее электрон и другие фермионы), но и такие макроскопические уравнения, как волновое уравнение, описывающее (приближенно) звук, колебания струн и мембран, и некоторые другие (только тогда уже в формулах преобразований Лоренца под c следует иметь в виду не скорость света, а какую-то другую константу, например скорость звука). Поэтому преобразования Лоренца могут быть плодотворно использованы и в связи с такими уравнениями (хотя и в довольно формальном смысле, впрочем, мало отличающемся — в своих рамках — от их применения в фундаментальной физике). [править]Вид преобразований при коллинеарных (параллельных) пространственных осях Если ИСО
где Эта форма преобразования (то есть при выборе коллинеарных осей), называемая иногда бустом (англ. boost) или лоренцевским бустом (особенно в англоязычной литературе), несмотря на свою простоту, включает, по сути, всё специфическое физическое содержание преобразований Лоренца, так как пространственные оси всегда можно выбрать таким образом, а при желании добавить пространственные повороты не представляет трудности (см. это в явном развёрнутом виде ниже), хотя и делает формулы более громоздкими. § Формулы, выражающие обратное преобразование, то есть выражающие § Надо иметь в виду, что в литературе преобразования Лоренца часто записывается для упрощения в системе единиц, где § Видно, что при преобразованиях Лоренца события, одновременные в одной системе отсчёта, не являются одновременными в другой (относительность одновременности), кроме того, у движущегося тела сокращается продольный размер по сравнению с тем, какой оно имеет в сопутствующей ему системе отсчёта (лоренцево сокращение), а ход движущихся часов замедляется, если наблюдать их из «неподвижной» системы отсчёта (релятивистское замедление времени). [править]Вывод преобразований Основная статья: Вывод преобразований Лоренца Преобразования Лоренца могут быть получены абстрактно, из групповых соображений (в этом случае они получаются с неопределённым Надо заметить, что если не ограничивать класс преобразований координат линейными, то первый закон Ньютона выполняется не только для преобразований Лоренца, а для более широкого класса дробно-линейных преобразований [3](однако этот более широкий класс преобразований — за исключением, конечно, частного случая преобразований Лоренца — не сохраняет метрику постоянной). [править]Разные формы записи преобразований [править]Вид преобразований при произвольной ориентации осей В силу произвольности введения осей координат, многие задачи можно свести к указанному случаю. Если же задача требует иного расположения осей, то можно воспользоваться формулами преобразований в более общем случае. Для этого радиус-вектор точки
где
Тогда преобразования получат вид
где Эти формулы для случая параллельных осей, но с произвольно направленной скоростью, можно преобразовать к виду, впервые полученному Герглоцем:
Обратите внимание, что самый общий случай, когда начала координат не совпадают в нулевой момент времени, здесь не приведён с целью экономии места. Его можно получить, добавив к преобразованиям Лоренца трансляцию(смещение начала координат). [править]Преобразования Лоренца в матричном виде Для случая коллинеарных осей преобразования Лоренца записываются в виде
где При произвольной ориентации осей, в форме 4-векторов это преобразование записывается как:
где E — единичная матрица 3 Надо иметь в виду, что в литературе матрица преобразований Лоренца часто записывается для упрощения в системе единиц, где Произвольное однородное преобразование Лоренца можно представить как некоторую композицию вращений пространства и элементарных преобразований Лоренца, затрагивающих только время и одну из координат. Это следует из алгебраической теоремы о разложении произвольного вращения на простые. [править]Свойства преобразований Лоренца § Можно заметить, что в случае, когда § Преобразования Лоренца сохраняют инвариантным интервал для любой пары событий (точек пространства-времени) — то есть любой пары точек пространства-времени Минковского: § В частности, инвариантность интервала имеет место и для случая § Другие инвариантные гиперповерхности однородных преобразований Лоренца (аналоги сферы для пространства Минковского) — гиперболоиды: двуполостный гиперболоид для времениподобных интервалов относительно начала координат, и однополостный — для пространственноподобных интервалов. § Матрицу преобразования Лоренца при коллинеарных пространственных осях (в системе единиц c=1) можно представить как:
где § Если принять введённые Минковским обозначения [править]Следствия преобразований Лоренца Изменение длины Пусть в системе отсчета
или
Таким образом, длина движущегося стержня, измеренная «неподвижными» наблюдателями, оказывается меньше, чем собственная длина стержня. [править]Относительность одновременности Если два разнесённых в пространстве события (например, вспышки света) происходят одновременно в движущейся системе отсчёта, то они будут неодновременны относительно «неподвижной» системы. При Δt' = 0 из преобразований Лоренца следует Если Δx = x2 − x1 > 0, то и Δt = t2 − t1 > 0. Это означает, что, с точки зрения неподвижного наблюдателя, левое событие происходит раньше правого (t2 > t1). Относительность одновременности приводит к невозможности синхронизации часов в различных инерциальных системах отсчёта во всём пространстве. Пусть в двух системах отсчёта, вдоль оси x расположены синхронизированные в каждой системе часы, и в момент совпадения «центральных» часов (на рисунке ниже) они показывают одинаковое время. Левый рисунок показывает, как эта ситуация выглядит с точки зрения наблюдателя в системе S. Часы в движущейся системе отсчёта показывают различное время. Находящиеся по ходу движения часы отстают, а находящиеся против хода движения опережают «центральные» часы. Аналогична ситуация для наблюдателей в S' (правый рисунок). [править]Замедление времени для движущихся тел [править]Связанные определения Лоренц-инвариантность — свойство физических законов записываться одинаково во всех инерциальных системах отсчета (с учетом преобразований Лоренца). Принято считать, что этим свойством должны обладать все физические законы, и экспериментальных отклонений от него не обнаружено. Однако некоторые теории пока не удаётся построить так, чтобы выполнялась Лоренц-инвариантность. [править]История Преобразования названы в честь их первооткрывателя — Х. А. Лоренца, который впервые ввел их (вместо преобразований Галилея) в качестве преобразований, связывающих геометрические величины (длины, углы), измеренные в разных инерциальных системах отсчета[источник не указан 293 дня], чтобы устранить противоречия между электродинамикой и механикой, которые имелись в ньютоновской формулировке, включающей преобразования Галилея, что в конечном итоге привело к успеху при существенной модификации механики. Сначала было обнаружено, что уравнения Максвелла инвариантны относительно подобных преобразований (В. Фогтом в 1887 году)[источник не указан 293 дня]. Это же было повторено Лармором в 1900 году[источник не указан 293 дня]. В 1892 году Лоренц ввёл теорию сокращения, предполагающую сокращение длин всех твёрдых тел в направлении движения, количественно совпадающее с тем, что понимается сейчас под лоренцевым сокращением. Преобразования Лоренца были впервые опубликованы Лоренцем в 1904 году, но в то время их форма была несовершенна (они были выведены с точностью до членов Пуанкаре же ввел термины «преобразования Лоренца» и «группа Лоренца» и показал, исходя из эфирной модели, невозможность обнаружить движение относительно абсолютной системы отсчета (то есть системы, в который эфир неподвижен), модифицировав таким образом принцип относительности Галилея[источник не указан 293 дня]. Ему же принадлежит групповой вывод явного вида преобразований Лоренца (с неопределенным c) без независимого постулата инвариантности скорости света[источник не указан 293 дня]. В 1910 году В.С. Игнатовский первым попытался получить преобразование Лоренца на основе теории групп и без использования постулата о постоянстве скорости света [5].
15. Относительность отрезков длины и промежутков времени в СТО. Собственное время. Релятивистский закон преобразования скоростей. Относительность длин и промежутков времени. [1] Оботносительности длин и промежутков времени. Последующие рассуждения основываются на принципе относительности и на принципе постоянства скорости света. [2] Из определения длины следует, чтоотносительность длины данного стержня является следствием относительности понятия одновременности. Это же относится и к форме любого тела - его размеры в направлении движения также различны в разных инерциальных системах отсчета. [3] Рассматриваются различные следствия из этих преобразований: относительность длин тел, моментов и промежутков времени. Рассматривается также сложное движение в релятивистской кинематике. [4] Преобразования Лоренца и следствия из них приводят к выводу оботносительности длин и промежутков времени, значение которых в различных системах отсчета разное. [5] Нетрудно видеть, что эти уравнения эквивалентны изложенным выше выводам оботносительности длин и промежутков времени. [6] Постулаты Эйнштейна и теория, построенная на их основе, установили новый взгляд на мир и новые пространственно-временные представления, такие, например, какотносительность длин и промежутков времени, относительность одновременности событий. Эти и другие следствия из теории Эйнштейна находят надежное экспериментальное подтверждение, являясь тем самым обоснованием постулатов Эйнштейна - обоснованием специальной теории относительности. [7] Наряду с безусловно положительными результатами, принесенными теорией относительности в физику, имеются попытки иска зить физическое содержание этой теории с целью обоснования чисто идеалистических, махистских воззрений. Относительность длины тела и промежутка времени при инерциальных движениях подменяют истолкованием этих величин как субъективных понятий. На этом основании физики-махисты отрицают объективный характер законов природы. [8] Между формулами (153.4) и (153.5) нет противоречия, ибо каждый раз имеются в виду различные измерения, хотя процедура измерений относительно каждой системы совершенно одинакова. В каждой системе получаем одинаковый результат; относительность длины, как и относительность времени, взаимна. [9] Обобщая полученные результаты, можно сделать вывод, что интервал, определяя пространственно-временные соотношения между событиями, является инвариантом при переходе от одной инерциальной системы отсчета к другой. Инвариантность интервала означает, что, несмотря наотносительность длин и промежутков времени, течение событий носит объективный характер и не зависит от системы отсчета. [10] Далее Эйнштейн с удивительным для первой работы изяществом доказывает достаточность названных двух постулатов. В Кинематической части работы он определяет одновременность; говорит оботносительности длин и времени; дает теорию преобразования координат и времени от покоящейся системы к системе, находящейся в равномерном поступательном движении относительно первой; физическое значение полученных уравнений для движущихся твердых тел и движущихся часов; выводит теорему сложения скоростей. [11] Поскольку формой существования всех видов материи является пространство - время, естественно включить в число основных единицы протяженности и времени. Здесь уместно сделать следующее замечание. Хотя с точки зрения теорииотносительности длины отрезков и промежутков времени утратили свою абсолютность, поскольку они зависят от относительного движения систем отсчета, они сохранили свою объективность, подобно тому как в обычной геометрии проекции отрезка на координатные оси, будучи относительными ( т.е. зависящими от системы координат), тем не менее остаются объективными. Эти соображения позволяют нам без всяких оговорок включить в число основных единицы длины и времени. То же в полной мере относится и к третьей величине - массе, единицы которой обычно также выбираются в качестве основных. [12] Собственное время в теории относительности, время, измеряемое часами в собственной системе отсчёта движущегося тела, т. е. часами, жёстко связанными с телом (покоящимися относительно него и находящегося в том же месте). Время протекания какого-либо процесса, измеряемое наблюдателем вне тела, в котором происходит процесс, зависит от относительной скорости наблюдателя и тела. При измерениях вдали от тяготеющих тел можно пользоваться частной (специальной) теорией относительности (см. Относительности теория). Если измерения производятся в некоторой инерциальной системе отсчета («лабораторной системе»), а тело движется относительно неё с постоянной скоростью u, то промежуток Собственное время Dt связан с промежутком времени Dt наблюдателя соотношением:
При наличии полей тяготения следует пользоваться общей теорией относительности (см. Тяготение). Собственное время процесса в поле тяготения течёт тем медленнее с точки зрения наблюдателя вне поля, чем сильнее гравитационное поле, т. е. чем больше модуль гравитационного потенциала j (потенциал j отрицателен, вне поля полагают j = 0). Для не слишком сильных полей, когда |j|/с2 << 1, Собственное время Dt по неподвижным часам в точке с потенциалом j связано с временем Dt неподвижного наблюдателя вне поля соотношением: Dt = (1 - |j|/c2)/Dt. Как видно из формул, Собственное время всегда меньше времени, измеренного в любой др. системе отсчёта.
16. Релятивистская форма второго закона Ньютона. Связь массы и энергии.
Поиск по сайту: |
 каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично, преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.
каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично, преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора. движется относительно ИСО
движется относительно ИСО  с постоянной скоростью
с постоянной скоростью  вдоль оси
вдоль оси  , а начала пространственных координат совпадают в начальный момент времени в обеих системах, то преобразования Лоренца (прямые) имеют вид:
, а начала пространственных координат совпадают в начальный момент времени в обеих системах, то преобразования Лоренца (прямые) имеют вид: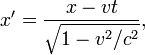



 — скорость света, величины со штрихами измерены в системе
— скорость света, величины со штрихами измерены в системе  через
через  можно получить просто заменой
можно получить просто заменой  (абсолютная величина относительной скорости движения систем отсчёта
(абсолютная величина относительной скорости движения систем отсчёта 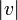 одинакова при измерении её в обеих системах отсчёта, поэтому можно при желании снабдить
одинакова при измерении её в обеих системах отсчёта, поэтому можно при желании снабдить  с нештрихованными. Или решая систему уравнений (1) относительно
с нештрихованными. Или решая систему уравнений (1) относительно  , что действительно делает их вид более изящным.
, что действительно делает их вид более изящным.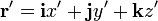 ,
, — орты, надо разбить на составляющую
— орты, надо разбить на составляющую  параллельную скорости и составляющую
параллельную скорости и составляющую  ей перпендикулярную
ей перпендикулярную .
. ,
,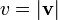 — абсолютная величина скорости,
— абсолютная величина скорости,  — абсолютная величина продольной составляющей радиус-вектора.
— абсолютная величина продольной составляющей радиус-вектора.
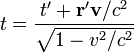 .
. ,
, .
.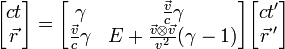

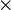 3,
3,  — тензорное умножение трехмерных векторов.
— тензорное умножение трехмерных векторов. , преобразования Лоренца переходят в преобразования Галилея. То же самое происходит в случае, когда
, преобразования Лоренца переходят в преобразования Галилея. То же самое происходит в случае, когда  . Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона либо в мире с бесконечной скоростью света, либо при скоростях, малых по сравнению со скоростью света. Последее объясняет, каким образом сочетаются эти две теории — первая является обобщением и уточнением второй, а вторая — предельным случаем первой, оставаясь в этом качестве верной приближенно (с некоторой точностью, на практике часто очень и очень большой) при достаточно малых (по сравнению со скоростью света) скоростях движений.
. Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона либо в мире с бесконечной скоростью света, либо при скоростях, малых по сравнению со скоростью света. Последее объясняет, каким образом сочетаются эти две теории — первая является обобщением и уточнением второй, а вторая — предельным случаем первой, оставаясь в этом качестве верной приближенно (с некоторой точностью, на практике часто очень и очень большой) при достаточно малых (по сравнению со скоростью света) скоростях движений.
 ортогональна в смысле метрики Минковского
ортогональна в смысле метрики Минковского
 . Это проще всего проделать для буста, а для трехмерных вращений это очевидно из определения декартовых координат, кроме того, сдвиги начала отсчёта не меняют разностей координат. Следовательно, это свойство верно и для любых композиций бустов, вращений и сдвигов, что и составляет полную группу Пуанкаре; как только мы узнали, что преобразования координат ортогональны, из этого сразу следует, что формула для расстояния остаётся неизменной при переходе к новой системе координат — по определению ортогональных преобразований.
. Это проще всего проделать для буста, а для трехмерных вращений это очевидно из определения декартовых координат, кроме того, сдвиги начала отсчёта не меняют разностей координат. Следовательно, это свойство верно и для любых композиций бустов, вращений и сдвигов, что и составляет полную группу Пуанкаре; как только мы узнали, что преобразования координат ортогональны, из этого сразу следует, что формула для расстояния остаётся неизменной при переходе к новой системе координат — по определению ортогональных преобразований.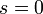 , а значит — гиперповерхность в пространстве-времени, которая определяется равенством нулю интервала до заданной точки — световой конус — является неподвижной при преобразованиях Лоренца (что является проявлением инвариантности скорости света). Внутреность двух полостей конуса соответствует времениподобным — вещественным — интервалам от их точек до вершины, внешняя область — пространственноподобным — чисто мнимым (в принятой в этой статье сигнатуре интервала).
, а значит — гиперповерхность в пространстве-времени, которая определяется равенством нулю интервала до заданной точки — световой конус — является неподвижной при преобразованиях Лоренца (что является проявлением инвариантности скорости света). Внутреность двух полостей конуса соответствует времениподобным — вещественным — интервалам от их точек до вершины, внешняя область — пространственноподобным — чисто мнимым (в принятой в этой статье сигнатуре интервала).
 . В этом легко убедиться, учитывая
. В этом легко убедиться, учитывая  и проверив выполнение соответствующего тождества для матрицы преобразования Лоренца в обычном виде.
и проверив выполнение соответствующего тождества для матрицы преобразования Лоренца в обычном виде. , то преобразование Лоренца для такого пространства сводится к повороту на мнимый угол в плоскости, включающей ось
, то преобразование Лоренца для такого пространства сводится к повороту на мнимый угол в плоскости, включающей ось 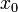 (для случая движения вдоль оси
(для случая движения вдоль оси 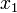 — в плоскости
— в плоскости  ). Это очевидно, исходя из подстановки
). Это очевидно, исходя из подстановки  в матрицу, приведенную чуть выше — и её небольшого изменения для того, чтобы учесть вводимую мнимость временной координаты — и сравнении её с обычной матрицей вращения.
в матрицу, приведенную чуть выше — и её небольшого изменения для того, чтобы учесть вводимую мнимость временной координаты — и сравнении её с обычной матрицей вращения. ,
, 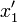 . Для определения длины стержня в системе
. Для определения длины стержня в системе 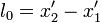 — собственная длина стержня в
— собственная длина стержня в  — длина стержня в
— длина стержня в 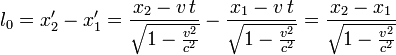
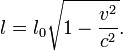
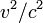 , а в преобразовании тока была допущена ошибка). К современному, полностью самосогласованному виду их привели французский математик А. Пуанкаре и параллельно и независимо А. Эйнштейн в 1905 году. Анри Пуанкаре первым установил и детально изучил одно из самых важных свойств преобразований Лоренца — их групповую структуру, и показал, что "преобразования Лоренца представляют ни что иное, как поворот в пространство четырех измерений, точки которого имеют координаты
, а в преобразовании тока была допущена ошибка). К современному, полностью самосогласованному виду их привели французский математик А. Пуанкаре и параллельно и независимо А. Эйнштейн в 1905 году. Анри Пуанкаре первым установил и детально изучил одно из самых важных свойств преобразований Лоренца — их групповую структуру, и показал, что "преобразования Лоренца представляют ни что иное, как поворот в пространство четырех измерений, точки которого имеют координаты  ".[4]. В 1905 году Эйнштейн в своей теории относительности пришёл к широко популярной впоследствии формально-аксиоматической трактовке этих преобразований.
".[4]. В 1905 году Эйнштейн в своей теории относительности пришёл к широко популярной впоследствии формально-аксиоматической трактовке этих преобразований. , где c - скорость света в вакууме; если u меняется со временем то для конечного интервала времени t1, t2 Собственное время
, где c - скорость света в вакууме; если u меняется со временем то для конечного интервала времени t1, t2 Собственное время