 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Математическое определение
Сила Кориолиса равна:
где Величина [править]Правило Жуковского Н. Е. Жуковским была предложена удобная для практического использования словесная формулировка определения силы Кориолиса Ускорение Кориолиса [править]Получение Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта S' со скоростью Тогда линейная скорость тела в неподвижной инерциальной системе координат равна:
где
Найдём значение каждого слагаемого в инерциальной системе координат:
где Таким образом, получаем:
Слагаемое Заметим, что если система S также является неинерциальной и движется относительно другой системы, а та другая относительно следующей и т. д., то величины Заметим также, что в частности, чтобы тело относительно неинерциальной системы отсчета двигалось прямолинейно по радиусу к оси вращения (см. рис.), необходимо приложить к нему силу, которая будет противодействующей суммы Кориолисовой силы [править]Физический смысл Пусть тело движется со скоростью Тогда данное движение приведёт к изменению расстояния до центра вращения Как мы знаем, эта скорость движения равна Данное изменение будет равно:
Проведя дифференцирование по времени, получим С другой стороны, вектор
Общее ускорение будет Если тело движется перпендикулярно направлению к центру вращения, то доказательство будет аналогичным. Ускорение из-за поворота вектора скорости останется [править]Сила Кориолиса в природе Сила Кориолиса, вызванная вращением Земли, может быть замечена при наблюдении за движением маятника Фуко[1]. Кроме того, сила Кориолиса проявляется и в глобальных масштабах. В северном полушарии сила Кориолиса направлена вправо от движения, поэтому правые берега рек в Северном полушарии более крутые — их подмывает вода под действием этой силы[2] (см. Закон Бэра). В Южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за вращение циклонов и антициклонов[3] (см. геострофический ветер): в Северном полушарии вращение воздушных масс происходит в циклонах против часовой стрелки, а в антициклонах — по стрелке; в Южном — наоборот: по часовой стрелке в циклонах и против — в антициклонах. Отклонение ветров (пассатов) при циркуляции атмосферы — также проявление силы Кориолиса. Если бы рельсы были бы идеальными, то при движении железнодорожных составов с севера на юг и с юга на север, под воздействием силы Кориолиса один рельс изнашивался бы сильнее, чем второй. В северном полушарии больше изнашивается правый, а в южном левый[4]. Силу Кориолиса необходимо учитывать при рассмотрении планетарных движений воды в океане. Она является причиной возникновения гироскопических волн[5]. При идеальных условиях сила Кориолиса определяет направление закручивания воды например, при сливе в раковине. Однако идеальные условия трудно достижимы. Поэтому феномен «обратного закручивания воды при стоке» является скорее околонаучной шуткой.
Маятник Фуко́ — маятник, используемый для экспериментальной демонстрации суточного вращения Земли. Эксперимент Фуко Впервые публичная демонстрация была осуществлена французским физиком и астрономом Жаном Фуко в 1851 г. в Парижском Пантеоне: под куполом Пантеона он подвесил металлический шар массой 28 кг с закреплённым на нём остриём на стальной проволоке длиной 67 м, крепление маятника позволяло ему свободно колебаться во всех направлениях, под точкой крепления было сделано круговое ограждение диаметром 6 метров, по краю ограждения была насыпана песчаная дорожка таким образом, чтобы маятник в своём движении мог при её пересечении прочерчивать на песке отметки. Чтобы избежать бокового толчка при пуске маятника, его отвели в сторону и привязали верёвкой, после чего верёвку пережгли. Период колебания маятника при такой длине подвеса составлял 16,4 секунд, при каждом колебании отклонение от предыдущего пересечения песчаной дорожки составляло ~3 мм, за час плоскость колебаний маятника повернулась более чем на 11° по часовой стрелке, то есть примерно за 32 часа совершила полный оборот и вернулась в прежнее положение. Физика эксперимента Маятник Фуко является математическим маятником, такой маятник, отклонённый от равновесного положения, совершает колебания в плоскости, неподвижной в инерциальной системе отсчёта (в данном случае — системе отсчёта, «связанной» со звёздами) и проявляет, таким образом, свойства гироскопа. Наблюдатель, находящийся на Земле и вращающийся вместе с нею, находится в неинерциальной (вращающейся) системе отсчёта и будет видеть, что плоскость колебаний маятника медленно поворачивается относительно земной поверхности в сторону, противоположную направлению вращения Земли. На Северном или Южном полюсе Земли (ось вращения Земли лежит в плоскости колебаний маятника) плоскость колебаний маятника Фуко совершает поворот на 360° за звёздные сутки (на 15° зазвёздный час), на экваторе (ось вращения Земли перпендикулярна плоскости колебаний маятника) плоскость колебаний маятника Фуко неподвижна, в произвольной точке с географическойширотой
Для неидеального маятника Фуко скорость вращения плоскости колебаний зависит и от длины подвеса:
где [править]Действующие маятники Фуко (в России и СНГ) По длине нити. § 24 февраля 2011 года модель маятника появилась в Киеве. Он установлен в Киевском политехническом институте. Шар из бронзы весит 43 килограмма, а длина нити составляет 22 метра. Киевский маятник Фуко считается самым большим в СНГ и одним из самых крупных в Европе[2]. § 12 июня 2011 года открылся Московский планетарий, где установлен действующий маятник Фуко с длиной нити 16 метров, массой шара - 50 килограммов[3]. § 8 февраля 2012 года открылся Новосибирский астрофизический комплекс, включающий в себя башню Фуко с маятником, длина нити которого 15 метров[4]. § Действующий маятник Фуко c длиной нити 20 метров имеется в Сибирском федеральном университете (Красноярск)[5]. § Действующий маятник Фуко, массой 12 килограммов и длиной нити 8,5 метров, имеется в Волгоградском планетарии[6]. § Действующий маятник Фуко в настоящее время есть в Санкт-Петербургском планетарии. Длина его нити — 8 метров[1]. § В Беларуси маятники Фуко установлены в Белорусском государственном педагогическом университете имени Максима Танка (длина нити — 7,5 метров) [7] и в каплице на мемориальном комплексе «Буйничское поле» (Могилёв) [8]. § Ещё один маятник Фуко находится в Барнауле в АлтГТУ им. И. И. Ползунова на кафедре экспериментальной физики в 403 аудитории. Длина его нити составляет 5,5 метра[9]. § Действующий маятник Фуко в настоящее время есть в Техническом Университете Молдовы[источник не указан 118 дней] [править]Интересные факты § Один из элементарных способов решения занимательной задачи П. Л. Капицы об облачности Венеры является измерение длины суток при помощи маятника Фуко[10]. Текст задачи: Астрономические наблюдения показывают, что на планете Венера полная облачность, так что «жители» Венеры лишены возможности наблюдать небесные светила. Опишите, каким методом они могли бы точно измерить длину своих суток.[11] § В Исаакиевском соборе в Ленинграде маятник Фуко был запущен в ночь с 11 на 12 апреля 1931 года. Тогда это назвали триумфом науки над религией. Однако представители церкви отметили, что этот опыт никак не опровергает догмат существования Бога. Хранитель экспозиции Исаакиевского собора Сергей Окунев прокомментировал это так: На самом деле, всё было наоборот. Первый опыт Фуко был выполнен с благословения папы Римского для того, чтобы доказать могущество Бога. 13. Постулаты специальной теории относительности. Системы отсчета в специальной теории относительности. Синхронизация часов. 1. Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна. Ключевым для аксиоматики специальной теории относительности является принцип относительности, утверждающий равноправие инерциальных систем отсчёта. Это означает, что все физические процессы в инерциальных системах отсчёта описываются одинаковым образом. Совместно с остальными постулатами, перечисленными выше, принципа относительности достаточно, чтобы получить явный вид преобразований координат и времени между ИСО [10] [12] [13]. Для этого необходимо рассмотреть три инерциальные системы S1, S2 и S3. Пусть скорость системы S2 относительно системы S1 равна
Доказательство[показать] Так как относительные скорости систем отсчёта Существование обратного преобразования между ИСО, отличающегося от прямого только заменой знака относительной скорости, позволяет найти функцию Доказательство[показать] Таким образом, с точностью до произвольной константы
и называются преобразованиями Лоренца. Из дальнейшего анализа станет ясно, что константа
2. Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую. Исторически важную роль при построении СТО сыграл второй постулат Эйнштейна, утверждающий, что скорость света Необходимо отметить, что световые сигналы, вообще говоря, не требуются при обосновании СТО. Хотя неинвариантность уравнений Максвелла относительно преобразований Галилея привела к построению СТО, последняя имеет более общий характер и применима ко всем видам взаимодействий и физических процессов. Фундаментальная константа В СТО постулируется возможность определения единого времени в рамках данной инерциальной системы отсчёта. Для этого вводится процедура синхронизации двух часов, находящихся в различных точках ИСО [5]. Пусть от первых часов, в момент времени Предполагается, что такая процедура в данной инерциальной системе отсчёта может быть проведена для любых неподвижных относительно друг друга часов, так что справедливо свойство транзитивности: если часы A синхронизованы с часами B, а часы B синхронизованы с часами C, то часы A и C также окажутся синхронизованными. В отличие от классической механики единое время можно ввести только в рамках данной системы отсчёта. В СТО не предполагается, что время является общим для различных систем. В этом состоит основное отличие аксиоматики СТО от классической механики, в которой постулируется существование единого (абсолютного) времени для всех систем отсчёта.
14. Относительность одновременности. Преобразования Лоренца и их следствия. Относительность одновременности событий является ключевым эффектом СТО, проявляющимся, в частности, в «парадоксе близнецов». Рассмотрим несколько синхронизированных часов, расположенных вдоль оси
Предположим, что рядом с каждыми часами в обеих системах отсчёта находятся наблюдатели. Положив в преобразованиях Лоренца Единое «настоящее», то есть часы, синхронно идущие в различных точках пространства, можно ввести только в рамках конкретной инерциальной системы отсчёта. Однако, этого нельзя сделать одновременно для двух различных систем отсчёта. Движущаяся относительно неподвижных наблюдателей система с их точки зрения содержит рассинхронизированные в направлении движения часы, своеобразное непрерывное объединение «прошлого», «настоящего» и «будущего». Эффекты замедления времени и относительности одновременности тесно связаны друг с другом и одинаково необходимы для расчёта ситуации, описанной в «парадоксе» близнецов.
Преобразова́ния Ло́ренца — линейные (или аффинные) преобразования векторного (соответственно, аффинного) псевдоевклидова пространства, сохраняющее длины или, что эквивалентно, скалярное произведение векторов. Преобразования Лоренца псевдоевклидова пространства сигнатуры (n-1,1) находят широкое применение в физике, в частности, в специальной теории относительности (СТО), где в качестве аффинного псевдоевклидова пространствавыступает четырёхмерный пространственно-временной континуум (пространство Минковского).
Поиск по сайту: |
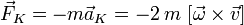 ,
,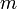 — точечная масса,
— точечная масса, 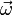 — вектор угловой скорости вращающейся системы отсчёта,
— вектор угловой скорости вращающейся системы отсчёта, 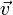 — вектор скорости движения точечной массы в этой системе отсчёта, квадратными скобками обозначена операция векторного произведения.
— вектор скорости движения точечной массы в этой системе отсчёта, квадратными скобками обозначена операция векторного произведения. называется кориолисовым ускорением.
называется кориолисовым ускорением.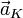 можно получить, спроецировав вектор скорости материальной точки в неинерциальной системе отсчёта
можно получить, спроецировав вектор скорости материальной точки в неинерциальной системе отсчёта 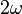 раз и повернув её на 90 градусов в направлении переносного вращения.
раз и повернув её на 90 градусов в направлении переносного вращения.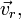 S' при этом сама движется поступательно с абсолютной линейной скоростью
S' при этом сама движется поступательно с абсолютной линейной скоростью  и одновременно вращается с угловой скоростью
и одновременно вращается с угловой скоростью 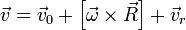 , причем
, причем 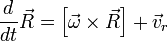
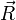 — радиус-вектор центра масс тела относительно неинерциальной системы отсчета S'. Продифференцируем данное уравнение:
— радиус-вектор центра масс тела относительно неинерциальной системы отсчета S'. Продифференцируем данное уравнение:
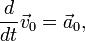

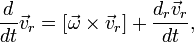
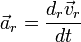 — линейное ускорение тела относительно системы S' в предположении ее неподвижности,
— линейное ускорение тела относительно системы S' в предположении ее неподвижности, 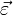 — угловое ускорение системы S' .
— угловое ускорение системы S' .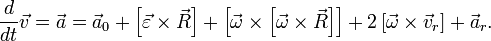
 и будет кориолисовым ускорением, образованном от взаимного влияния переносного поворотного и относительного поступательного движений.
и будет кориолисовым ускорением, образованном от взаимного влияния переносного поворотного и относительного поступательного движений.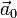 — абсолютным ускорением поступательного движения S' относительно неподвижной инерциальной системы координат.
— абсолютным ускорением поступательного движения S' относительно неподвижной инерциальной системы координат.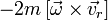 , переносной вращательной силы
, переносной вращательной силы 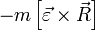 и переносной силы инерции поступательного движения системы отсчета
и переносной силы инерции поступательного движения системы отсчета 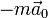 . Составляющая же ускорения
. Составляющая же ускорения 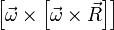 не отклонит тело от этой прямой так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нем вышеупомянутых сил получится уравнение
не отклонит тело от этой прямой так как является осестремительным переносным ускорением и всегда направлена по этой прямой. Действительно, если рассматривать уравнение такого движения, то после компенсации в нем вышеупомянутых сил получится уравнение  , которое если умножить векторно на
, которое если умножить векторно на  получим относительно
получим относительно  дифур
дифур 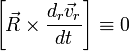 , имеющий при любых
, имеющий при любых 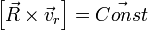 , которое и является уравнением такой прямой —
, которое и является уравнением такой прямой — 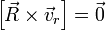 .
. и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой - ее переносной скорости.
и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой - ее переносной скорости.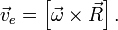

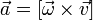 (направление данного ускорения перпендикулярно
(направление данного ускорения перпендикулярно  . Или приращение скорости будет
. Или приращение скорости будет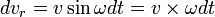 при
при  соответственно второе ускорение будет:
соответственно второе ускорение будет: Как видно, система отсчёта не претерпела изменения угловой скорости
Как видно, система отсчёта не претерпела изменения угловой скорости 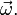 Линейная скорость относительно неё не меняется и остаётся
Линейная скорость относительно неё не меняется и остаётся  Тем не менее, ускорение не равно нулю.
Тем не менее, ускорение не равно нулю. а также прибавляется ускорение в результате изменения центростремительного ускорения точки.
а также прибавляется ускорение в результате изменения центростремительного ускорения точки. (угол между осью вращения Земли и плоскостью колебаний маятника
(угол между осью вращения Земли и плоскостью колебаний маятника 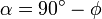 ) скорость вращения плоскости колебаний идеального маятника Фуко
) скорость вращения плоскости колебаний идеального маятника Фуко 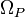 (в градусах в звёздный час) относительно поверхности Земли составляет
(в градусах в звёздный час) относительно поверхности Земли составляет

 — амплитуда колебаний груза маятника;
— амплитуда колебаний груза маятника;  — длина нити. Поэтому для демонстраций применяют маятники с максимально возможной длиной подвеса; так, в Исаакиевском соборе в Ленинградедемонстрировался маятник Фуко на подвесе длиной 98 м.
— длина нити. Поэтому для демонстраций применяют маятники с максимально возможной длиной подвеса; так, в Исаакиевском соборе в Ленинградедемонстрировался маятник Фуко на подвесе длиной 98 м. , скорость системы S3 относительно S2 равна
, скорость системы S3 относительно S2 равна  , а относительно S1, соответственно,
, а относительно S1, соответственно, 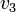 . Записывая последовательность преобразований (S2, S1), (S3, S2) и (S3, S1), можно получить следующее равенство [10]:
. Записывая последовательность преобразований (S2, S1), (S3, S2) и (S3, S1), можно получить следующее равенство [10]: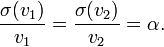
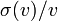 равно некоторой константе
равно некоторой константе  , единой для всехинерциальных систем отсчёта, и, следовательно,
, единой для всехинерциальных систем отсчёта, и, следовательно, 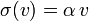 .
.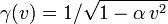 .
. , то удобно ввести обозначение
, то удобно ввести обозначение 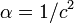 . Тогда преобразования принимают следующий вид:
. Тогда преобразования принимают следующий вид: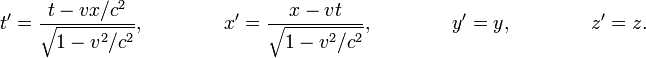
 имеет смысл максимальной скорости движения любого объекта. Подобный вывод преобразований Лоренца стал известен спустя 5 лет после известной статьи Эйнштейна 1905 года, благодаря работам Игнатовского[12], Франка и Роте [8] (см. исторический очерк).
имеет смысл максимальной скорости движения любого объекта. Подобный вывод преобразований Лоренца стал известен спустя 5 лет после известной статьи Эйнштейна 1905 года, благодаря работам Игнатовского[12], Франка и Роте [8] (см. исторический очерк). [16]. Первая константа отражает общие свойства пространства и времени, тогда как вторая связана со свойствами конкретного взаимодействия. Чтобы измерить фундаментальную скорость
[16]. Первая константа отражает общие свойства пространства и времени, тогда как вторая связана со свойствами конкретного взаимодействия. Чтобы измерить фундаментальную скорость  ко вторым посылается сигнал (не обязательно световой) с постоянной скоростью
ко вторым посылается сигнал (не обязательно световой) с постоянной скоростью  . Сразу по достижении вторых часов (по их показаниям в момент времени
. Сразу по достижении вторых часов (по их показаниям в момент времени  ) сигнал отправляется обратно с той же постоянной скоростью
) сигнал отправляется обратно с той же постоянной скоростью  . Часы считаются синхронизированными, если выполняется соотношение
. Часы считаются синхронизированными, если выполняется соотношение 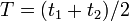 .
. в каждой из систем отсчёта. В преобразованиях Лоренца предполагается, что в момент времени
в каждой из систем отсчёта. В преобразованиях Лоренца предполагается, что в момент времени 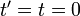 начала систем отсчёта совпадают:
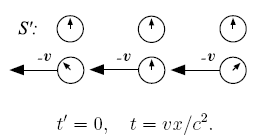
начала систем отсчёта совпадают:  . Ниже изображена такая синхронизация отсчёта времени (на «центральных» часах) с точки зрения системы отсчёта
. Ниже изображена такая синхронизация отсчёта времени (на «центральных» часах) с точки зрения системы отсчёта 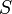 (левый рисунок) и с точки зрения наблюдателей в
(левый рисунок) и с точки зрения наблюдателей в 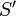 (правый рисунок):
(правый рисунок):
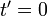 , получаем
, получаем 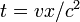 . Это означает, что наблюдатели в системе
. Это означает, что наблюдатели в системе 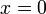 , с координатами
, с координатами 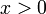 , в момент времени
, в момент времени 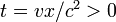 . Наблюдатели
. Наблюдатели  . На рисунках выше положение стрелок символизирует подобную разницу показаний часов двух систем отсчёта.
. На рисунках выше положение стрелок символизирует подобную разницу показаний часов двух систем отсчёта.