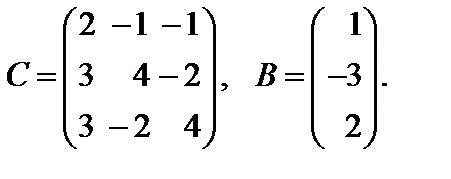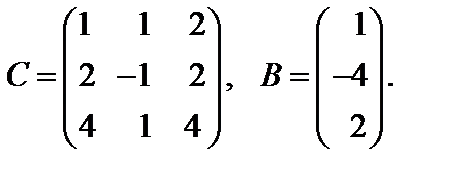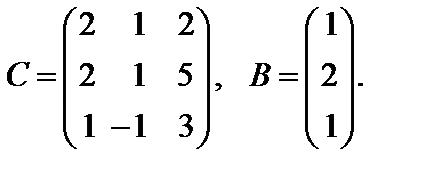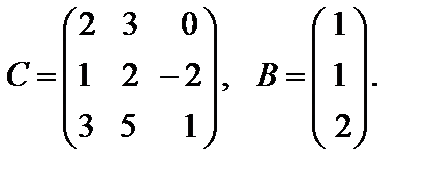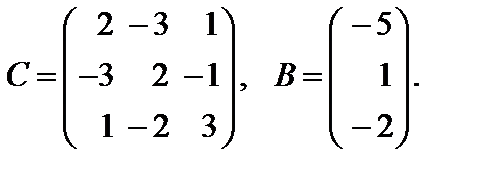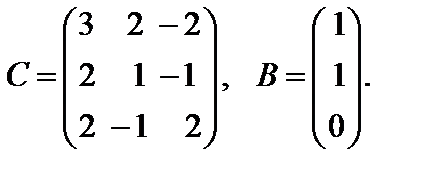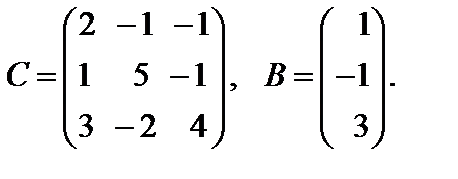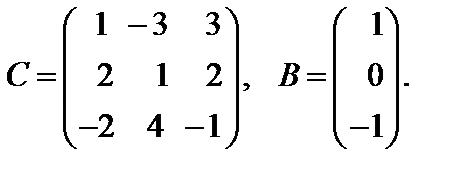|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Математические функции⇐ ПредыдущаяСтр 14 из 14
Принятые обозначения: x, y - действительные переменные; z - комплексная переменная; V - вектор; A,B,M - матрицы, i, j, k, n, m - целые переменные.
Тригонометрические функции sin(z) Синус cos(z) Косинус tan(z) Тангенс cot(z) Котангенс sec(z) Секанс csc(z) Косеканс
Гиперболические функции sinh(z) Гиперболический синус cosh(z) Гиперболический косинус tanh(z) Гиперболический тангенс coth(z) Гиперболический котангенс sech(z) Гиперболический секанс csch(z) Гиперболический косеканс
Обратные тригонометрические и гиперболические функции asin(z) Арксинус acos(z) Арккосинус atan(z) Арктангенс asinh(z) Гиперболический арксинус acosh(z) Гиперболический арккосинус atanh(z) Гиперболический арктангенс
Экспоненциальная и логарифмические функции exp(z) e в степени z ln(z) Натуральный логарифм log(z) Десятичный логарифм
Функции Бесселя J0(x) Функция Бесселя первого рода нулевого порядка Y0(x) Функция Бесселя второго рода нулевого порядка I0(x) Модифицированная функция Бесселя нулевого порядка K0(x) Модифицированная функция Ганкеля нулевого порядка J1(x) Функция Бесселя первого рода первого порядка Y1(x) Функция Бесселя второго рода первого порядка I1(x) Модифицированная функция Бесселя первого порядка K1(x) Модифицированная функция Ганкеля первого порядка Jn(m, x) Функция Бесселя первого рода m - го порядка Yn(m, x) Функция Бесселя второго рода m - го порядка In(m, x) Модифицированная функция Бесселя m - го порядка Kn(m, x) Модифицированная функция Ганкеля m - го порядка
Функции комплексных величин Re(z) Вещественная часть z Im(z) Мнимая часть z arg(z) Аргумент z
Условные функции if(cond, tval, fval) Если условное выражение cond = 0, то tval, иначе fval until(expr1, expr2) expr2, пока expr1 >= 0 d(m,n) 1, если m = n, и 0 в других случаях e(i,j,k) Антисимметричный тензор ранга 3 F(x) Функция Хевисайда (единичная функция), равная 1 для x >= 0 и 0 для x < 0.
Функции операций с векторами и матрицами augment(A,B) Объединение двух матриц с одинаковым числом строк cols(M) Число столбцов матрицы M eigenvals(M) Вектор собственных значений матрицы M eigenvec(M,z) Собственный вектор матрицы M, соответствующий собственному значению z (собственное подпространство M, принадлежащее z) identity(n) Получение квадратной единичной матрицы n x n last(v) Номер последнего элемента в v length(v) Число элементов в v max(M) Наибольший элемент в M min(M) Наименьший элемент в M rows(M) Число строк матрицы M tr(M) След матрицы M Другие функции ceil(x) Наименьшее целое, большее или равное x (например, ceil(3.4) = 4) floor(x) Наибольшее целое, меньшее или равное x (например, floor(3.4) = 3) mod(x,y) Остаток от деления x/y со знаком x (например, mod(2,6) = 2) angle(x,y) Положительный угол между осью x и точкой (x,y), в радианах (например angle(-6,0) = 3.14159 Приложение 7 Варианты к лабораторной работе №11. (п.1)
Варианты к лабораторной работе №11. (п. 2) Найти неопределенные интегралы. Результаты проверить дифференцированием.
Варианты к лабораторной работе №11. (п. 3) Найти матрицу
Литература
[1] Острейковский В.А. Информатика: Учеб. для вузов. – М.: Высш. шк., 2001. – 501 с.
Поиск по сайту: |







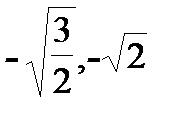



 3у2 – 4х2 - 12
3у2 – 4х2 - 12






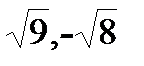

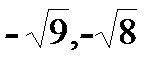












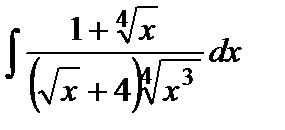



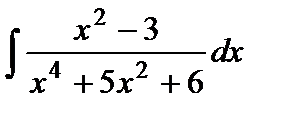


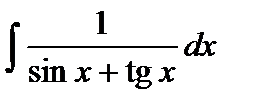





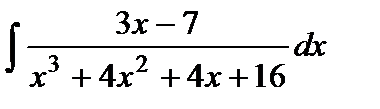
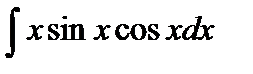

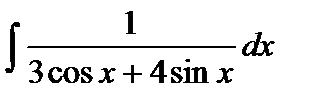

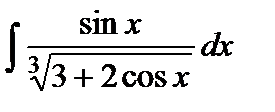



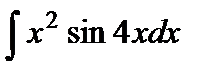

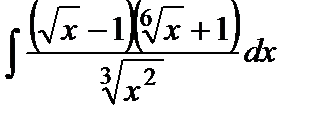



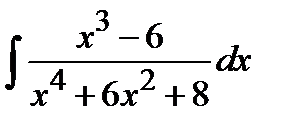




 и произведение матриц С·В
и произведение матриц С·В