Тренировочная задача 1

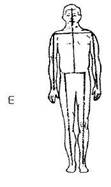
Предположим, вы наблюдаете в теле векторно-осевую систему, представленную на рисунке Ш-8. Как поступить?

Я вижу два способа начала исправления. Во-первых, можно при­ступить к коррекции центрального вертикального вектора/оси сверху. В этом случае у вас будет выпрямленный центральный вертикальный вектор/ось, по которому выравнивается поперечный вектор/ось бедер. Преобразование нижнего поперечного вектора/оси выполняется легче.

1. Нарушение целостности определенного вектора/оси

2. Вектор/ось выпрямлен, но его концы еще не зацепились. Они только совмещены.

3. Концы Вектора/оси зацепились, целостность восстановлена.

4. Точка указывает ось поворота. Линия от точки до стрелки представляет предыдущее положение вектора/оси с имеющимся наклоном. Стрелки указывают расстояние и направление перестановки.

5. Направление силы, приложенной врачом.

6. Вращение участка сначала в одном направлении, а затемв другом для сцепления двух концов разорванного вектора/оси.

7. Аккумулирование энергии в точке разрыва, но разъединенные концы не сближаются.

1) Центральный вертикальный вектор/ось

разорван и наклонен в сторону.

2) Поперечный вектор/ось бедер наклонен

относительно центрального вертикального вектора/оси.

3) Вектор/ось правой ноги выходит за

границу ступни физического тела.

Рисунок Ш-8

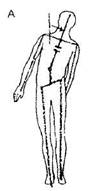
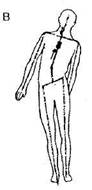
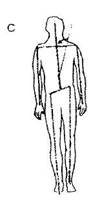
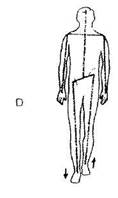
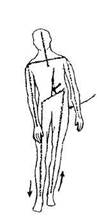
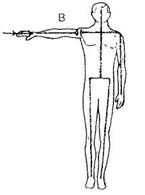
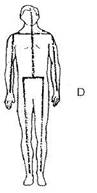
Какие шаги следует предпринять для соединения и выравнивания векторно-осевой системы этим способом?

Сдвигайте всю нижнюю часть тела пациента, пока не выпрямится нижний участок вектора, как показано на рисунке A (III-9). Одновре­менно двигайте правую ногу вверх, а левую оттягивайте вниз, чтобы вектор/ось бедер образовал прямой угол с нижней частью центрального вертикального вектора, рисунок В. Но сначала потребуется вытянуть правую ногу и сдвинуть вверх левую, чтобы вектор/ось вернулся в тело, как показано на рисунке А. После этого нужно поменять направления вытягиваия и сдвигания, чтобы векторая система заняла в теле положе­ние, как показано на рисунке В.

Изменение положения нижней части физического тела изменяет положение векторно-осевой системы тела. Используйте пересечения средней линии и центрального вертикального вектора/оси как ось поворота, чтобы соединить концы центрального вертикального вектора/ оси, как показано на рисунке С. Подождите, пока положение вектора стабилизируется, рисунок D.

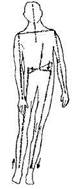
Рисунок Ш-9. Исправление векторно-осевой системы способом 1, тренировочная задача 1

Второй вариант предполагает одновременную коррекцию поперечного вектора/оси бедер и устранение наклона нижней части центрального вертикального вектора/оси (рисунок III-10). Затем соединяется разрыв на среднем участке центрального вертикального вектора/оси.

Не могу сказать, какой вариант лучше. Второй способ более слож­ный, поскольку требует одновременного выполнения двух процедур, но это более интересно. Если не получится с первого раза, попробуйте еще. Никакого вреда от этого нет, так что у вас неограниченное число возможностей справиться с задачей.

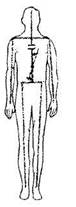
Рисунок Ш-10. Коррекция векторно-осевой системы способом 2, описанным в тренировочной задаче 1

Тренировочная задача 2

Ситуация похожа на первый случай (рисунок III-11). Так оно и есть. Здесь кроется маленькая хитрость, позволяющая добиться хоро­шего результата. Как только рука окажется на одном уровне с плечом, ее нужно повернуть так, как вкручивается конечность у манекена. Помните, плечи и бедра имеют шарниры, так что придется немного покрутить руку, чтобы найти положение соединения.

Рисунок III-11

Рисунок III — 11. Коррекция разрыва векторно-осевой системы в правом плече.

Тренировочная задача 2

Поиск по сайту: