 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интегрирование рациональных выражений
Разложение многочлена на множители: Опр. 1: Алгебраическим многочленом n-й степени с действительными коэффициентами наз. выражение Pn(x)=anxn+an-1xn-1+... +a1x+a0 [1], где an¹0, an-1,... ,a0 [1] - постоянные действительные числа, а x - переменное действительное число. Теор. №1 (без док.): любой многочлен Pn(x), n³1 из [1] с вещественными коэффициентами представим в виде Pn(x)=an(x–b1)k1 ×(x–b2)k2... (x–bmkm)(x2+p1x+g1)l1... (x2+psx+gs)ls [2], где b1, b2, bm - корни многочлена Pn(x), а квадратные трехчлены x2+pix+gi с действительными коэффициентами не имеют действительных корней и n=k1+k2+... +km+2(l1+l2+... +ls). Число x=b наз. корнем многочлена Pn(x), если Pn(b)=0. Разложение неправильной рац. дроби на сумму многочлена и прав. рац. дроби: Опр. 2: рациональной дробью R(x) наз. отнош. многочленов R(x)=Pn(x)/Qm(x) [3]. Если n³m, то дробь наз. неправильной, если n£m, то дробь наз. правильной. Любую неправильную дробь [2] можно представить в виде суммы многочлена и правильной рациональной дроби: если n³m, то Pn(x)/Qm(x)=Tn-m(x)+rk(x)/Qm(x) [4], где k<m. Представление [4] можно получить с помощью деления многочлена на многочлен "уголком". Частное служит многочленом Tn-m(x), а остаток - многочленом rk(x).
Разложение правильной рац. дроби на простейшие: Теор. №2 (без док.): пусть R(x)= R(x)=Pn(x)/Qm(x) - правильная рациональная дробь и Qm(x)=(x–b1)k1...(x–bj)kj(x2+p1x+g1)l1... (x2+psx+gs)ls [5]. Тогда эта правильная дробь представима в виде суммы простейших дробей: В этом разложении Bij, Mij, Nij - некоторые действительные постоянные, часть из которых может обратиться в нуль. Поясним, что каждая скобка из [5] порождает столько слагаемых в [6], какова её степень. Линейным скобкам соответствуют слагаемые, у которых в числителях стоят константы, а скобкам с квадратными трехчленами соответствуют слагаемые, у которых числители являются линейными двучленами. Для фактического нахождения коэффициентов Bij, Mij, Nij можно привести правую часть [6] к общему знаменателю и приравнять выражения при одинаковых степенях x в числителях. В результате подучится линейная система уравнений, из которой коэффициенты Bij, Mij, Nij определяются однозначно. Этот способ наз. методом неопределенных коэффициентов. Иногда часть коэффициентов можно найти методом вычеркивания: для определения коэффициента Blkl в левой части [6] вычёркивается скобка (x–bl)kl в знаменателе. В оставшемся выражении полагают x=bl. Получившееся число и будет равно Blkl. Интегрирование простейших дробей: Неправильная рациональная дробь представима в виде суммы многочлена и правильной рациональной дроби. В результате интегрирования многочлена получается тоже многочлен, но степени на единицу выше. Правильная рациональная дробь разлагается на сумму простейших дробей. Если мы сумеем найти интегралы от простейших дробей, то проблема интегрирования произвольной рациональной дроби решена. В силу разложения [6] простейшие дроби бывают следующих четырех типов:1) B/x–b; 2) B/(x–b)k, k>1; 3) Mx+N/x2+px+q; 4) Mx+N/(x2+px+q)k , k>1. Здесь b, B, p, q, M, N - некоторые вещественные числа, k - натуральное число и квадратный трехчлен (x2+px+q) не имеет вещественных корней. Каждая из указанных простейших дробей интегрируется в элементарных функциях: 1) ò(B/(x–b))dx=ln|x–b|+c; 2) ò(B/(x–b)k)dx=–B×1/(k–1)(x–b)k–1+c, k>1. 3) Для вычисления простейшей дроби третьего типа нужно выделить квадрат в знаменателе и сделать соответствующую замену переменных. 4) Вычисление интеграла вида òMx+N/(x2+px+q)kdx сводится к вычислению интеграла вида òMx+N/(x2+px+q)k-1dx и т.д., пока получится интеграл третьего вида, который свободно вычисляется. Теор. №3: всякая рациональная дробь интегрируема в элементарных функциях. Билет 27 Интегрирование тригонометрических выражений: Многие интегралы с помощью замены переменной можно свести к интегралу от рациональной функции. Универсальная тригонометрическая подстановка: R(u,v) - рациональная функция двух переменных т.е. отношение многочленов двух переменных. Т.к. рациональная функция от рациональной функции есть тоже рациональная функция и произведение рациональных функций представляет собой рациональную функцию, то полученный интеграл для переменной t есть интеграл от рациональной функции. Замена переменной, допустим t=tg(x/2) - наз. универсальной тригонометрической подстановкой. Вычисление интегралов вида òsinnx×cosmx dx, n,mÎZ: а) Хотя бы одно из чисел n, m - нечётное. Пусть для определения n=2k+1. Тогда òsin2k+1x×cosmx dx=–òsin2kx×cosmx d(cosx)= –ò(1–cos2x)k×cosmx d(cos x)= –ò(1–t2)ktmdt. При преобразовании использована замена t=cos x. Т.о. в этом случае исходный интеграл сводится к интегралу от многочлена. б) Оба числа m, n - чётные. В этом случае нужно понижать степень с помощью формул: cos2x=1+cos2x/2; sin2x=1–cos2x/2. Вычисление интегралов вида òsinax×sinbx dx, òsinax×cosbx dx, òcosax×cosbx dx: Для вычисления этих интегралов надо использовать формулы преобразования произведения тригонометрических функций в сумму . Интегрирование иррациональных выражений: Интегрирование дробно-линейных иррациональностей: Пусть R(u,v) - рациональная функция двух переменных. Покажем, что вычисление интеграла вида òR(x,2Öax+b/2Öcx+d)dx, где n - натуральное число, a, b, c, d - вещественные числа, сводится к вычислению интеграла от рациональной функции. Для этого сделаем замену t=nÖax+b/2Öcx+d. Тогда x=dtn–b/a–ctn, dx=(ad–bc)ntn-1dt/(a–ctn)2. Поэтому òR(x,2Öax+b/2Öcx+d)dx=òR(dtn–b/a–ctn, t)((ad–bc)ntn-1 dt/(a–ctn)2)dt. Интеграл в правой части равенства есть интеграл от рациональной функции. Интегрирование биноминальных дифференциалов: Рассмотрим интегралы вида òxm(a+bxn)pdx, где a, b - любые действительные числа, m, n, p - некоторые рациональные числа. Подинтегральное выражение в рассматриваемом интеграле наз. биномиальным дифференциалом. 1) p - целое число. Тогда интеграл рационализируется (сводится к интегралу от рациональной функции) подстановкой t=rÖx, где r - наименьшее общее кратное знаменателей рациональных чисел m и n. 2) (m+1)/n - целое число. Интеграл от дифференциального бинома сводится к интегралу от дробно-линейной иррациональности подстановкой Z=xn. 3) ((m+1)/n)+p - целое число. В этом случае исходный интеграл тоже сводится к интегралу от дробно-линейной иррациональности с помощью той же замены переменной Z=xn. Интегрирование квадратичных иррациональностей: Пусть R(u,v) - рациональная функция двух переменных. Докажем интегрируемость в элементарных функциях интегралов вида òR(x,Öax2+bx+c)dx. Для этого выделим в подкоренном выражении полный квадрат и с помощью замены переменных приведём корень к одному из следующих видов: Öa2+t2, Öa2–t2, Öt2–d2. Далее сделаем тригонометрическую подстановку: в первом случае t=dtgu,во втором t=dsinu, в третьем t=d/cosu. В результате придём к интегралу от тригонометрической функции вида òR(sinu,cosu)du, где R(u,v) - некоторая новая рациональная функция двух переменных. Такой интеграл, заведомо рационализируется с помощью универсальной тригонометрической подстановки.
Билет 28 Пусть даны две непрерывные на [a, b] функции f1(x) f2(x), и нам надо найти площадь между ними в пределах отрезка [a, b]. Как это сделать, говорит следующая лемма. Лемма Усл. Функции f1(x) f2(x) заданы и непрерывны на [a, b]. Утв.Площадь фигуры , ограниченной графиками f1(x) и f2(x), а также прямыми x = a и x = b, вычисляется по формуле: S= Доказательство Обозначим искомую плoщадь между графиками через S, площадь под гра- фиком функции f1(x) через S1, а площадь под графиком функции f2(x) Через S2. Очевидно, что S1 = S + S2 C другой стороны, S1 = S = рицательны. Случаи, когда обе они неположительны, одна из них или обе меняют знак на промежутке (a, b), рассматриваются полностью аналогично. Только надо учитывать, что итеграл от функции по промежутку, где она отрицательна, будет равен площади со знаком минус соответствуюющей фигуры, оказавшейся под осью Ox
Поиск по сайту: |

 =(f2(x) - f1(x)) dx
=(f2(x) - f1(x)) dx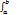 f1(x)dx, а S2 =
f1(x)dx, а S2 =  (f2(x) - f1(x)) dx. ЗамечаниеПриведённое доказательство соответствует случаю, когда обе функции f1(x) и f2(x) неот-
(f2(x) - f1(x)) dx. ЗамечаниеПриведённое доказательство соответствует случаю, когда обе функции f1(x) и f2(x) неот-