Билет 10 производная обратной функции

Производная обратной функции равна обратной величине производной данной функции =

Основные формулы:

Для сложных функций:

Билет 11Пусть функция y = f ( x ) дифференцируема на некотором отрезке [ a , b ]. Значения производной f'(x) зависят от х, т.е. производная f'(x) тоже представляет собой некоторую функцию от х. Дифференцируя эту функцию, мы получаем производную от производной.

О. Производная от первой производной называется производной второго порядка или второй производной. Обозначается

y''=( f'( x ))'= f''( x ). (4.5)

Физический смысл второй производной: вторая производная f''(x) равна скорости изменения скорости, т.е. ускорению движущейся точки в момент времени х.

Вторая производная также может быть функцией, определенной на некотором множестве. Если эта функция имеет производную, то эта производная называется третьей производной функции f(x) и обозначается f'''(x).

О. Если определена ( n -1) -я производная f (n -1 ) (x) и существует её производная, то она называется n-й производной функции f(x):

f ( n ) ( x ) = ( f ( n -1 ) ( x ))' . (4.6)

Все производные, начиная со второй, называются производными высших порядков.

Функцию, имеющую на данном множестве конечную производную порядка n , называют n раз дифференцируемой на данном множестве.

Дифференциал функции y = f ( x ) выражается в виде dy = f'( x ) dx . Тогда, если он является некоторой функцией от х, то справедливо следующее:

О. Дифференциал от дифференциала функции называется дифференциалом второго порядка или вторым дифференциалом:

d 2 y = f''( x ) dx 2 . (4.7)

О. Дифференциал от дифференциала n -го порядка называется дифференциалом ( n +1)-го порядка.

Билет 19Направление выпуклости. Точки перегиба. Необходимое и достаточное условия. Исследование по высшей производной.

Линия называется выпуклой, если она пересекается с любой своей секущей не более чем в 2х точках. Линия называется вогнутой, если она целиком лежит по 1 сторону от касательной, проведенной в любой ее точке.

Точка перегиба - точка, отделяющая выпуклый участок дуги от вогнутого.

Необходимый признак выпуклости и вогнутости: если линия на интервале выпуклая, то ее 2я производная <=0; если линия на интервале вогнутая, то ее f``(x)>=0

Достаточный признак: если f``(x) всюду в интервале “-”, то линия в интервале выпуклая; если f``(x)>0, то линия вогнутая.

Признаки точки перегиба: чтобы X₀ была т. перегиба, <=> чтобы у`` в этой точке = 0 и меняла знак при переходе х через

Билет 20Исследование функции на экстремум с помощью производных высших порядков

Пусть в точке х = х1 f¢(x1) = 0 и f¢¢(x1) существует и непрерывна в некоторой окрестности точки х1.

Теорема. Если f¢(x1) = 0, то функция f(x) в точке х = х1 имеет максимум, если f¢¢(x1)<0 и минимум, если f¢¢(x1)>0.

Доказательство.

Пусть f¢(x1) = 0 и f¢¢(x1)<0. Т.к. функция f(x) непрерывна, то f¢¢(x1) будет отрицательной и в некоторой малой окрестности точки х1.

Т.к. f¢¢(x) = (f¢(x))¢ < 0, то f¢(x) убывает на отрезке, содержащем точку х1, но f¢(x1)=0, т.е. f¢(x) > 0 при х<x1 и f¢(x) < 0 при x>x1. Это и означает, что при переходе через точку х = х1 производная f¢(x) меняет знак с “+” на “-“, т.е. в этой точке функция f(x) имеет максимум.

Для случая минимума функции теорема доказывается аналогично.

Поиск по сайту:
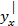