 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сема построения графика
Найти область определения функции. Найти область значений функции. Обычно этот пункт пропускают или заполняют после исследования на экстремумы. Исследовать непрерывность функции, выделить особые точки (точки разрыва). Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения. Найти точки пересечения с осями координат. Найти нули функции. Найти интервалы знакопостоянства функции. Установить, является ли функция чётной или нечётной. Сделать выводы о симметричности графика функции. Установить, является ли функция периодической или нет. Обычно проверяют для тригонометрических функций, для других данный пункт пропускается. Найти первую производную. Найти точки экстремума (локального минимума и максимума) и интервалы монотонности (возрастания и убывания) функции. Найти вторую производную. Найти точки перегиба и интервалы выпуклости-вогнутости. Найти наклонные/горизонтальные асимптоты функции. Исследовать поведение функции на бесконечности. Построить график функции. Построить асимптоты. Отметить важные точки на графике.
Билет 21Первообразная функция. Определение: Функция F(x) называется первообразной функциейфункции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство: F¢(x) = f(x). Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число. F1(x) = F2(x) + C. постоянная. Теор: пусть F1(х) и F2(x) - любые первообразные для функции ¦(x) на (a,b). Тогда всюду на этом интервале F1(х)–F2(x)=C, где С - некоторая константа. Док: введем функцию Ф(x)=F1(х)–F2(x). Производная этой функции = 0 на (a,b): Ф'(x)=F'1(х)–F'2(x)=¦(x)–¦(x)=0. => что есть константа на (a,b). В самом деле. Пусть x0 - любая, но фиксированная точка интервала (a,b). С помощью теоремы Лагранжа выразим разность значений функций Ф(х)–Ф(х0), где Х - любая точка (a,b): Ф(x)–Ф(x0)=Ф'(x)(x–x0)=0×(x–x0)=0. В последней формуле x - точка, расположенная между x и x0. Полагая С=Ф(х0), имеем Ф(х)=Ф(х0)=C, т.е. F1(х)–F2(x)=C. Теор. док. Следствие: Если F(x) - первообразная функция для ¦(x) на (a,b), то любая другая первообразная Ф(x) для ¦(x) на (a,b) представима в виде Ф(x)=F(x)+C, где С - некоторая константа. Определение: Совокупность всех первообразных функций для функции ¦(x) на (a,b) наз. неопределенным интегралом от функции ¦(x) и обознач: ò¦(x)dx. При этом знак ò наз. знаком интеграла, выражение ¦(x)dx наз. подъинтегральным выражением, а ¦(x) подъинтегральной функцией. В силу следствия теоремы о первообразных можно записать ò¦(x)dx=F(x)+C [1], где F(x) - какая-нибудь первообразная для ¦(x) на (a,b), а С - любая Основные свойства неопределенного интеграла: Непосредственно из определения следуют свойства: 1) dò¦(x)dx=¦(x)dx; 2) òdF(x)= F(x)+C. Для доказательства свойства 1) достаточно продифференцировать формулу [1]: d(ò¦(x)dx)= d(F(x)+C)= (F'+C')dx=¦(x)dx. Доказательство свойства 2) тоже основано на той же формуле 1), только нужно учесть, что dF(x)=¦(x)dx. Cвойства 1), 2) означают, что знаки d и ò взаимно сокращаются, только во втором случае еще добавляется слагаемым произвольная постоянная. Следующие два свойства наз. линейными свойствами неопределенного интеграла: 3) ò(¦(x)+g(x))dx=ò¦(x)dx+òg(x)dx; 4) òA¦(x)dx=Aò¦(x)dx, A=const. Доказательство свойств 3), 4) основано на факте, который уже использовался при доказательстве теоремы №1: если производные двух функций на интервале (a,b) совпадают, то на этом интервале функции отличаются на константу. Нетрудно убедиться, что производные левой и правой частей равенства 3 совпадают. (ò(¦(x)+g(x))dx)'= (¦(x)+g(x))= (ò(¦(x)dx)'+(òg(x)dx)'= (ò¦(x)+òg(x)dx)'. Стало быть свойство 3) имеет место. Аналогично доказывается свойство 4). Билет 22Способ подстановки (замены переменных неопред интеграл).
Теорема: Если требуется найти интеграл Доказательство: Продифференцируем предлагаемое равенство: По рассмотренному выше свойству №2 неопределенного интеграла: f(x)dx = f[j(t)]j¢(t)dt что с учетом введенных обозначений и является исходным Интегрирование по частям. Способ основан на известной формуле производной произведения: (uv)¢ = u¢v + v¢u где u и v – некоторые функции от х. В дифференциальной форме: d(uv) = udv + vdu Проинтегрировав, получаем: Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Билет 23
Поиск по сайту: |
 , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается: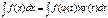

 , а в соответствии с приведенными выше свойствами неопределенного интеграла:
, а в соответствии с приведенными выше свойствами неопределенного интеграла: или
или  ;
;