 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Формула Ньютона – Лейбница
Пусть в интеграле а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла. Обозначим
Аналогичную теорему можно доказать для случая переменного нижнего предела. Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл. Теорема: (Теорема Ньютона – Лейбница) Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то
это выражение известно под названием формулы Ньютона – Лейбница. Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция
при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:
Тогда А при х = b: Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:
Билет 25 Замена переменной в определённом интеграле: Теор: пусть 1) Функция ¦(t) непрерывна на [a,b]. 2) Отрезок [a,b] явл. множеством значений функции t=g(x), xÎ[a,b], причём g'(x) непрерывна на [a,b]. 3) g(a)=a; g(b)=b. Тогда òab¦(t)dt=òab¦(g(x))g'(x)dx [1] -формула замены переменной под знаком определенного интеграла. Док: пусть F(t)- некоторая первообразная функции ¦(t) на отрезке [a,b] (она существует в силу непрерывности ¦(t)). Тогда òab¦(t)dt=F(b)–F(a) [2]. Функция F(t) дифференцируема на [a,b], поэтому дифференцируема и функция F(g(x)), отрезке [a,b], причем dF(g(x))/dx=F'(g(x))g'(x)= ¦(g(x))g'(x). Стало быть по формуле Ньютона-Лейбница, òab¦(g(x))g'(x)=F(g(b))–F(g(a))= F(b)–F(a) [3] Сравнивая формулы [2] и [3], получаем [1]. Теор. док. Вычисление определённого интеграла по частям: Теор: Пусть функции u(x) и v(x)имеют непрерывные производные на отрезке [a,b]. Тогда справедлива формула òabu(x)v'(x)dx=u(x)v(x)|ab–òabv(x)u'(x)dx [1]. - формула интегрирования по частям для определенного интеграла и записывают её еще в виде òabudv=uv|ab–òabvdu. Док: заметим, что функция u(x) и v(x) явл. первообразной для функции (uv)'=u'v+uv', причем эта функция непрерывна. => òab(u'(x)v(x)+u(x)v'(x))dx= (u(x)v(x))|ab [2]. Т.к. u'(x)v(x), u(x)v'(x) - непрерывные на [a,b] функции, то определённые интегралы от этих функций сущ. и формулу [2] можно записать в форме [1]. Теор. док. 25 билет Интегрирование по частям .определённый интеграл
Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:
Замена переменных. Пусть задан интеграл Введем новую переменную в соответствии с формулой x = j(t). Тогда если 1) j(a) = а, j(b) = b 2) j(t) и j¢(t) непрерывны на отрезке [a, b] 3) f(j(t)) определена на отрезке [a, b], то
Тогда Билет 26
Поиск по сайту: |
 нижний предел
нижний предел = Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.
= Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.

 - первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то
- первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то


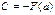
 .
.


 , где f(x) – непрерывная функция на отрезке [a, b].
, где f(x) – непрерывная функция на отрезке [a, b].
